题目内容
当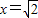 时,
时,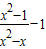 = .
= .
【答案】分析:先将分式的分子和分母分别分解因式,约分化简,然后将x的值代入化简后的代数式即可求值.
解答:解: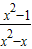 -1
-1
=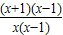 -1
-1
=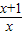 -
-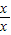
=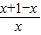
=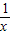 ,将x=
,将x=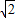 代入上式中得,
代入上式中得,
原式=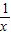 =
=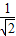 =
=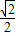 .
.
故答案为: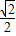 .
.
点评:本题主要考查分式求值方法之一:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.
解答:解:
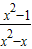 -1
-1=
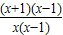 -1
-1=
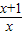 -
-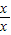
=
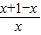
=
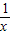 ,将x=
,将x=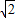 代入上式中得,
代入上式中得,原式=
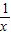 =
=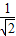 =
=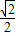 .
.故答案为:
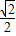 .
.点评:本题主要考查分式求值方法之一:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目