题目内容
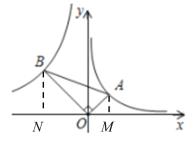
【题目】如图,在平面直角坐标系中,△AOB中,∠AOB=90°,∠ABO=30°,顶点A在反比例函y=![]() (x>0)上运动,此时顶点B也在反比例函数y=
(x>0)上运动,此时顶点B也在反比例函数y=![]() 上运动,则m的值为( )
上运动,则m的值为( )
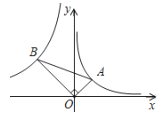
A.-9B.-12C.-15D.-18
【答案】A
【解析】
根据∠AOB=90°,∠ABO=30°,可求出OA与OB的比,设出点B的坐标,再根据相似三角形的性质,求出点A的坐标,可得ab的值,进而求出m的值.
解:过A、B分别作AM⊥x轴,BN⊥x轴,垂足为M、N,
∵∠AOB=90°,∠ABO=30°,
∴tan30°=![]() ,
,
∵∠BON+∠AOM=90°,∠BON+∠OBN=90°,
∴∠OBN=∠AOM,
∵∠BNO=∠AMO=90°,
∴△BNO∽△OMA,
∴![]() ,
,
∴设ON=a,BN=b,则AM=![]() ,OM=
,OM=![]() ,
,
∴B(-a,b),A(![]() ,
,![]() ),
),
∵点A在反比例函数y=![]() 上,
上,
则![]() ×
×![]() =3,
=3,
∴ab=9,
∵点B在反比例函数y=![]() 上,
上,
∴-a×b=m=-9,
故选A.

【题目】![]() 城有肥料
城有肥料![]() ,
,![]() 城有肥料
城有肥料![]() .现要把这些肥料全部运往
.现要把这些肥料全部运往![]() 、
、![]() 两乡,
两乡,![]() 乡需要肥料240t,
乡需要肥料240t,![]() 乡需要肥料
乡需要肥料![]() ,其运往
,其运往![]() 、
、![]() 两乡的运费如下表:
两乡的运费如下表:
两城/两乡 | C/(元/ | D/(元/ |
| 20 | 24 |
| 15 | 17 |
设从![]() 城运往
城运往![]() 乡的肥料为
乡的肥料为![]() ,从
,从![]() 城运往两乡的总运费为
城运往两乡的总运费为元,从
![]() 城运往两乡的总运费为
城运往两乡的总运费为![]() 元
元
(1)分别写出![]() 、
、![]() 与
与![]() 之间的函数关系式(不要求写自变量的取值范围);
之间的函数关系式(不要求写自变量的取值范围);
(2)试比较![]() 、
、![]() 两城总运费的大小;
两城总运费的大小;
(3)若![]() 城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.
城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.
【题目】某校组织全校学生进行了一次“社会主义核心价值观”知识竞赛,赛后随机抽取了各年级部分学生成绩进行统计,制作如下频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
分数段( | 频数 | 频率 |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
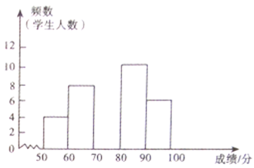
(1)请求出该校随机抽取了____学生成绩进行统计;
(2)表中![]() ____,
____,![]() ____,并补全直方图;
____,并补全直方图;
(3)若用扇形统计图描述此成绩统计分布情况,则分数段![]() 对应扇形的圆心角度数是___
对应扇形的圆心角度数是___![]() ;
;
(4)若该校共有学生8000人,请估计该校分数在![]() 的学生有多少人?
的学生有多少人?