题目内容
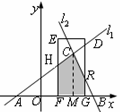
如图,已知直线![]() 与直线
与直线![]() 相交于点
相交于点![]() 分别交
分别交![]() 轴
轴![]() 两点.矩形
两点.矩形![]() 的顶点
的顶点![]() 分别在直线
分别在直线![]() 上,顶点
上,顶点![]() 都在
都在![]() 轴上,且点
轴上,且点![]() 与点
与点![]() 重合.
重合.

(1)求![]() 的面积;
的面积;
(2)求矩形![]() 的边
的边![]() 与
与![]() 的长;
的长;
(3)若矩形![]() 从原点出发,沿
从原点出发,沿![]() 轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t<3)秒,矩形
轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t<3)秒,矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 关于的函数关系式.
关于的函数关系式.
(1)36;(2)4,8;(3)![]()
【解析】
试题分析:(1)先分别求得两条直线与x轴的交点坐标,再求得两条直线的交点坐标,最后根据三角形的面积公式求解即可;
由![]() 得
得![]() 点坐标为
点坐标为![]()
(2)根据矩形的性质即可求的![]() 点的坐标,再根据点
点的坐标,再根据点![]() 在
在![]() 上即可求得
上即可求得![]() 点的坐标,即得结果;
点的坐标,即得结果;
(3)当![]() 时,如图,矩形
时,如图,矩形![]() 与
与![]() 重叠部分为五边形
重叠部分为五边形![]() (
(![]() 时,为四边形
时,为四边形![]() ).过
).过![]() 作
作![]() 于
于![]() ,证得
,证得![]() 再根据相似三角形的性质及三角形的面积公式求解即可.
再根据相似三角形的性质及三角形的面积公式求解即可.
(1)由![]() 得
得![]() 点坐标为
点坐标为![]()
由![]() 得
得![]() 点坐标为
点坐标为![]()
∴![]()
由 解得
解得![]()
∴![]() 点的坐标为
点的坐标为![]()
∴![]()
(2)∵点![]() 在
在![]() 上且
上且![]()
∴![]() 点坐标为
点坐标为![]()
又∵点![]() 在
在![]() 上且
上且![]()
∴![]() 点坐标为
点坐标为![]()
∴![]()
(3)当![]() 时,如图,矩形
时,如图,矩形![]() 与
与![]() 重叠部分为五边形
重叠部分为五边形![]() (
(![]() 时,为四边形
时,为四边形![]() ).过
).过![]() 作
作![]() 于
于![]() ,
,
则![]()
∴![]() 即
即![]() ∴
∴![]()
![]()
∴![]()
即![]()
考点:函数的综合题
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目

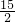 时,求直线a′的函数解析式;
时,求直线a′的函数解析式; 与直线
与直线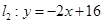 相交于点
相交于点 分别交
分别交 轴
轴 两点.矩形
两点.矩形 的顶点
的顶点 分别在直线
分别在直线 上,顶点
上,顶点 都在
都在 与点
与点 重合.
重合.
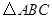 的面积;
的面积; 与
与 的长;
的长; ,求
,求 时,求直线a′的函数解析式;
时,求直线a′的函数解析式;
 与直线
与直线 相交于点
相交于点 分别交
分别交 轴
轴 两点.矩形
两点.矩形 的顶点
的顶点 分别在直线
分别在直线 上,顶点
上,顶点 都在
都在 与点
与点 重合.
重合.
 的面积;
的面积; 与
与 的长;
的长; ,求
,求