题目内容
在1998年的特大洪水期间，为了加固一段大堤，需运来沙石和土将大堤堤面加宽1米，使背水坡的坡度由原来的1：2变为1：3,已知原来背水坡的坡长为BC=15米，堤长100米，那么需要的沙石和土多少方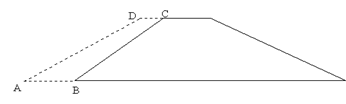
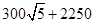方过C作CE⊥AB,垂足为E,设CE=x,则BE="2x,"
过D作DF⊥AB,垂足为F, 则DF="CE=x," AF=3x
∴AB=AF-BF=AF-(BE-EF)=3x-(2x-1)=x+1
∵Rt△CEB中， BC=15,x2+(2x)2=152,得： x=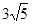
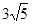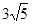, ∴CE=,AB=+1
∴S梯形ABCD=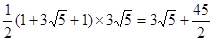
∴需沙石，土：V=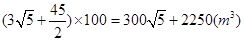
增加部分的截面为梯形ABCD，需要计算梯形ABCD的面积，依题意过C作CE⊥AB，垂足为E，设CE=x，则BE=2x，过D作DF⊥AB，垂足为F，则DF=CE=x，AF=3x，在Rt△CEB中，由勾股定理求DE，BE，再利用AB=AF-BF=AF-（BE-EF）=3x-（2x-1）=x+1，求AB，根据梯形面积公式求S梯形ABCD，由堤长100米求土方数．
过D作DF⊥AB,垂足为F, 则DF="CE=x," AF=3x
∴AB=AF-BF=AF-(BE-EF)=3x-(2x-1)=x+1
∵Rt△CEB中， BC=15,x2+(2x)2=152,得： x=
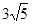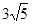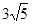, ∴CE=,AB=+1∴S梯形ABCD=
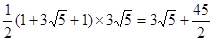
∴需沙石，土：V=
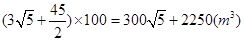
增加部分的截面为梯形ABCD，需要计算梯形ABCD的面积，依题意过C作CE⊥AB，垂足为E，设CE=x，则BE=2x，过D作DF⊥AB，垂足为F，则DF=CE=x，AF=3x，在Rt△CEB中，由勾股定理求DE，BE，再利用AB=AF-BF=AF-（BE-EF）=3x-（2x-1）=x+1，求AB，根据梯形面积公式求S梯形ABCD，由堤长100米求土方数．
练习册系列答案
相关题目
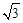≈1.732，结果保留三个有效数字）．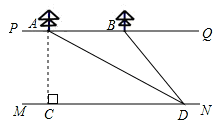
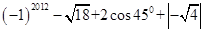．111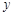
轴对称的点的坐标是
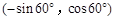，则点P关于x轴的对称点的坐标为（ ）
，
）
，
）
）
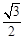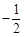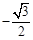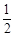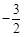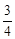，矩形BCDE的边CD=2BC，这个横截面框架（包括BE）所用的钢管总长为15m．求帐篷的篷顶A到底部CD的距离．（结果精确到0.1m）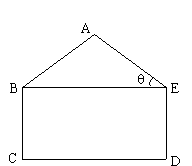
|
.
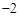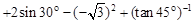