��Ŀ����
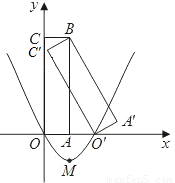
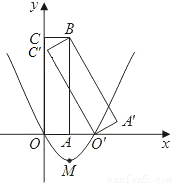
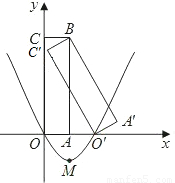
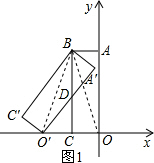
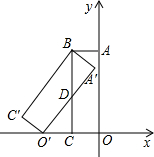 ��ͼ������A��BC��O���Ǿ���ABCO�Ƶ�B˳ʱ����ת�õ��ģ����е�O'��C��x�Ḻ�����ϣ��߶�OA��y���������ϣ�B�������Ϊ��-1��3����
��ͼ������A��BC��O���Ǿ���ABCO�Ƶ�B˳ʱ����ת�õ��ģ����е�O'��C��x�Ḻ�����ϣ��߶�OA��y���������ϣ�B�������Ϊ��-1��3������1��������κ���y=ax2+bx+c��a��0����ͼ��O��O��������ͼ��M��������Ϊ
-1����������κ����Ľ���ʽ��
��2�����O��A������ֱ�ߵĽ���ʽ��
��3���ڣ�1��������Ķ��κ���ͼ�����Ƿ���ڵ�P��ʹ��S��PO��M=3S��CO��D�������ڣ��������P�����꣬�������ڣ���˵�����ɣ�
��������1������BO��BO�䣬������ת�����ʿɵ�BO=BO�䣬�ٸ��ݶԳ��Կ�֪OC=O��C��Ȼ���ϵ�B�����������O��������Լ�����M�����꣬���ô���ϵ������������ʽ���ɣ�
��2�������ýǽDZ�֤����A��BD���CO��Dȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�BD=O��D��Ȼ����Rt��CDO���У����ù��ɶ������CD�ij��ȣ����ɵõ���D�����꣬�����ô���ϵ�������ֱ��O��A��Ľ���ʽ��
��3���������CO��D�������Ȼ����������ߵĽ���ʽ���P������Ϊ��x��x2+2x��������P��PQ��x�ύֱ��O��M�ڵ�Q�����ֱ��O��M�Ľ���ʽ��Ȼ�������Q������Ϊ��x��-x-2����Ȼ�����S��PO��M=S��PQM-S��PO��Q��Ȼ����������ε������ʽ�����õ�����x��һԪ���η��̣���⼴�ɵõ���P�����꣮
��2�������ýǽDZ�֤����A��BD���CO��Dȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�BD=O��D��Ȼ����Rt��CDO���У����ù��ɶ������CD�ij��ȣ����ɵõ���D�����꣬�����ô���ϵ�������ֱ��O��A��Ľ���ʽ��
��3���������CO��D�������Ȼ����������ߵĽ���ʽ���P������Ϊ��x��x2+2x��������P��PQ��x�ύֱ��O��M�ڵ�Q�����ֱ��O��M�Ľ���ʽ��Ȼ�������Q������Ϊ��x��-x-2����Ȼ�����S��PO��M=S��PQM-S��PO��Q��Ȼ����������ε������ʽ�����õ�����x��һԪ���η��̣���⼴�ɵõ���P�����꣮
����⣺��1����ͼ1������BO��BO�䣬����ת�����ʵ�BO=BO�䣬
��BC��OC��
��O��C=OC��
�ߵ�B������Ϊ��-1��3��������M��������Ϊ-1��
���O�䣨-2��0����M��-1��-1����
��
��
���
��
��������κ����Ľ���ʽΪy=x2+2x��
��2����ͼ1���ڡ�A��BD���CO��D�У�
��
���A��BD�ա�CO��D��AAS����
��BD=O��D��
��O��D=3-CD��
��Rt��CDO����O��D2=CD2+O��C2��
����3-CD��2=CD2+12��
���CD=
��
���D��������-1��
����
��ֱ��O��A��Ľ���ʽΪy=kx+b��
��
��
���
��
��ֱ��O��A��Ľ���ʽΪy=
x+
��
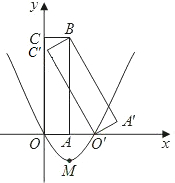
��3����ͼ2���ɵ�D������Ϊ��-1��
���ɵ�S��CO��D=
O��C•CD=
��1��
=
��
�����ڵ�P��ʹ��S��PO��M=3S��CO��D����S��PO��M=3��
=2��
��O�䣨-2��0����M��-1��-1���ã�
��
���
��
��ֱ��O��M�Ľ���ʽΪy=-x-2��
���P��������x��x2+2x����
����P��PQ��x�ύO��M�ڵ�Q�����Q������Ϊ��x��-x-2����
��S��PO��M=S��PQM-S��PO��Q��
��S��PO��M=
[��x2+2x��-��-x-2��]•[��-1-x��-��-2-x��]=2��
�����ã�x2+3x-2=0��
���x=
��
��x=
ʱ��y=x2+2x=
��
��x=
ʱ��y=x2+2x=
��
����ڵ�P1��
��
����P2��
��
����
��BC��OC��
��O��C=OC��
�ߵ�B������Ϊ��-1��3��������M��������Ϊ-1��
���O�䣨-2��0����M��-1��-1����
��
|

���
|
��������κ����Ľ���ʽΪy=x2+2x��
��2����ͼ1���ڡ�A��BD���CO��D�У�
|
���A��BD�ա�CO��D��AAS����
��BD=O��D��
��O��D=3-CD��
��Rt��CDO����O��D2=CD2+O��C2��
����3-CD��2=CD2+12��
���CD=
| 4 |
| 3 |
���D��������-1��
| 4 |
| 3 |
��ֱ��O��A��Ľ���ʽΪy=kx+b��
��
|
���
|
��ֱ��O��A��Ľ���ʽΪy=
| 4 |
| 3 |
| 8 |
| 3 |
��3����ͼ2���ɵ�D������Ϊ��-1��
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |

�����ڵ�P��ʹ��S��PO��M=3S��CO��D����S��PO��M=3��
| 2 |
| 3 |
��O�䣨-2��0����M��-1��-1���ã�
|
���
|
��ֱ��O��M�Ľ���ʽΪy=-x-2��
���P��������x��x2+2x����
����P��PQ��x�ύO��M�ڵ�Q�����Q������Ϊ��x��-x-2����
��S��PO��M=S��PQM-S��PO��Q��
��S��PO��M=
| 1 |
| 2 |
�����ã�x2+3x-2=0��
���x=
-3��
| ||
| 2 |
��x=
-3+
| ||
| 2 |
7-
| ||
| 2 |
��x=
-3-
| ||
| 2 |
7+
| ||
| 2 |
����ڵ�P1��
-3+
| ||
| 2 |
7-
| ||
| 2 |
-3-
| ||
| 2 |
7+
| ||
| 2 |
�����������ۺϿ����˶��κ��������⣬����ת�任�����ʣ�����ϵ��������κ�������ʽ����ֱ�ߵĽ���ʽ��ȫ�������ε��ж������ʣ������ε�������Լ����ε����ʣ��ۺ��Խ�ǿ���ѶȽϴ�3�������ú�������ʽ���ķ����Ƚ���Ҫ��Ҳ�����Ĺؼ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ʱ����ת�õ��ģ�O�����x����������ϣ�B�������Ϊ��1��3����
ʱ����ת�õ��ģ�O�����x����������ϣ�B�������Ϊ��1��3����