题目内容
【题目】如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：
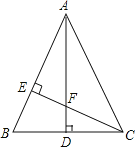
（1）△AEF≌△CEB；
（2）AF=2CD．
【答案】见解析
【解析】
试题分析：（1）由AD⊥BC，CE⊥AB，易得∠AFE=∠B，利用全等三角形的判定得△AEF≌△CEB；
（2）由全等三角形的性质得AF=BC，由等腰三角形的性质“三线合一”得BC=2CD，等量代换得出结论．
证明：（1）∵AD⊥BC，CE⊥AB，
∴∠BCE+∠CFD=90°，∠BCE+∠B=90°，
∴∠CFD=∠B，
∵∠CFD=∠AFE，
∴∠AFE=∠B
在△AEF与△CEB中，
，
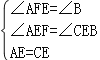∴△AEF≌△CEB（AAS）；
（2）∵AB=AC，AD⊥BC，
∴BC=2CD，
∵△AEF≌△CEB，
∴AF=BC，
∴AF=2CD．
练习册系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
