题目内容
6个人用35天完成了某项工程的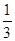
，如果再增加工作效率相同的8个人，那么完成这项工程，前后共用的天数是( )
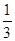，如果再增加工作效率相同的8个人，那么完成这项工程，前后共用的天数是( )| A．30 | B．40 | C．60 | D．65 |
考点：
专题：工程问题．
分析：应先算出一个人的工作效率，进而算出14个人的工作效率，还需要的天数=剩余的工作量÷14个人的工作效率，把相关数值代入即可求解．
解答：解：总工作量看做单位“1”．剩余工作量为1-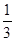
=
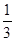，一个人的工作效率为÷6÷35，
∴还需（1-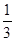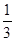）÷[÷6÷35×14]=30天，
共需要30+35=65天．
故选D．
点评：本题考查一元一次方程的应用，得到剩余工作量和14个人的工作效率是解决本题的关键；用到的知识点为：时间=工作总量÷工作效率．
专题：工程问题．
分析：应先算出一个人的工作效率，进而算出14个人的工作效率，还需要的天数=剩余的工作量÷14个人的工作效率，把相关数值代入即可求解．
解答：解：总工作量看做单位“1”．剩余工作量为1-
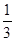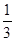=，一个人的工作效率为÷6÷35，∴还需（1-
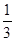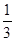）÷[÷6÷35×14]=30天，共需要30+35=65天．
故选D．
点评：本题考查一元一次方程的应用，得到剩余工作量和14个人的工作效率是解决本题的关键；用到的知识点为：时间=工作总量÷工作效率．
练习册系列答案
相关题目
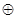”如下：当a≥b>0时，a
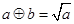，根据这个规则，方程(3
﹣
=5的解是（ ）
与
可以合并，则n= . 
人，则全班有（ ）人，