题目内容
已知矩形的两条对角线相交所成的一个角为120°,矩形的宽为4cm,则对角线的长为
- A.2cm
- B.4cm
- C.8cm
- D.16cm
C
分析:根据矩形的性质求得OA=OD,再根据已知条件,∠AOD=120°,AB=4cm,得到BD=2AB,即可求出矩形对角线AC的长.
解答:∵四边形ABCD是矩形,
∴AC=BD.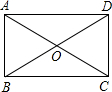
又∵OA=OC= AC,OB=OD=
AC,OB=OD= BD,
BD,
∴OA=OD.
∵∠AOD=120°,
∴∠ODA=∠OAD=30度.
又∵∠DAB=90°,
∴BD=2AB=2×4=8(cm).
故选C.
点评:本题主要考查矩形的性质的知识点,运用矩形的对角线相等且互相平分是解决本题的关键,此题比较简单.
分析:根据矩形的性质求得OA=OD,再根据已知条件,∠AOD=120°,AB=4cm,得到BD=2AB,即可求出矩形对角线AC的长.
解答:∵四边形ABCD是矩形,
∴AC=BD.

又∵OA=OC=
 AC,OB=OD=
AC,OB=OD= BD,
BD,∴OA=OD.
∵∠AOD=120°,
∴∠ODA=∠OAD=30度.
又∵∠DAB=90°,
∴BD=2AB=2×4=8(cm).
故选C.
点评:本题主要考查矩形的性质的知识点,运用矩形的对角线相等且互相平分是解决本题的关键,此题比较简单.

练习册系列答案
相关题目
已知矩形的两条对角线相交所成的一个角为120°,矩形的宽为4cm,则对角线的长为( )
| A、2cm | B、4cm | C、8cm | D、16cm |
已知矩形的两条对角线的夹角为60°,两条对角线的和为8,则矩形的周长为( )
A、2+4
| ||
B、2+2
| ||
C、4+4
| ||
D、4+2
|
已知矩形的两条对角线相交所成的一个角为120°,矩形的宽为4cm,则对角线的长为
| A.2cm | B.4cm | C.8cm | D.16cm |