题目内容
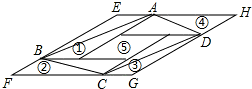 如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为28cm2,四边形ABCD面积是18cm2,则①②③④四个平行四边形周长的总和为
如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为28cm2,四边形ABCD面积是18cm2,则①②③④四个平行四边形周长的总和为
- A.72cm
- B.64cm
- C.56cm
- D.48cm
B
分析:求出⑤平行四边形的面积,求出菱形EFGH的面积,过E作EM⊥GH于M,设EH=HG=FG=EF=xcm,求出x的值,结合图形即可求出答案.
解答:∵①②③④四个平行四边形面积的和为28cm2,四边形ABCD面积是18cm2,
∴平行四边形⑤的面积是18- ×28=4(cm2),
×28=4(cm2),
∴菱形EFGH的面积是4+28=32cm2,
过E作EM⊥GH于M,
设EH=HG=FG=EF=xcm,
∵∠H=30°,
∴EM= x,
x,
即 x•x=32,
x•x=32,
x=8,
∴EH=HG=FG=EF=8cm,
∴①②③④四个平行四边形的周长的和正好是8×8=64,
故选B.
点评:本题考查了含30度角的直角三角形性质,平行四边形性质,菱形性质等知识点,能根据图形得出①②③④四个平行四边形的周长的和正好是8个EF是解此题的关键,注意:菱形的对边相等,平行四边形的对边相等.
分析:求出⑤平行四边形的面积,求出菱形EFGH的面积,过E作EM⊥GH于M,设EH=HG=FG=EF=xcm,求出x的值,结合图形即可求出答案.
解答:∵①②③④四个平行四边形面积的和为28cm2,四边形ABCD面积是18cm2,
∴平行四边形⑤的面积是18-
 ×28=4(cm2),
×28=4(cm2),∴菱形EFGH的面积是4+28=32cm2,
过E作EM⊥GH于M,
设EH=HG=FG=EF=xcm,
∵∠H=30°,
∴EM=
 x,
x,即
 x•x=32,
x•x=32,x=8,
∴EH=HG=FG=EF=8cm,
∴①②③④四个平行四边形的周长的和正好是8×8=64,
故选B.
点评:本题考查了含30度角的直角三角形性质,平行四边形性质,菱形性质等知识点,能根据图形得出①②③④四个平行四边形的周长的和正好是8个EF是解此题的关键,注意:菱形的对边相等,平行四边形的对边相等.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 如图,下列五个三角形中与第一个三角形相似的是( )
如图,下列五个三角形中与第一个三角形相似的是( )A、 | B、 | C、 | D、 |
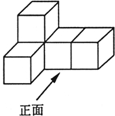 22、如图是由五个小正方体搭成的几何体,它的左视图是( )
22、如图是由五个小正方体搭成的几何体,它的左视图是( )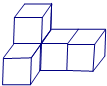 11、如图是由五个大小相同的正方体搭成的几何体,则关于它的视图,下列说法正确的是( )
11、如图是由五个大小相同的正方体搭成的几何体,则关于它的视图,下列说法正确的是( )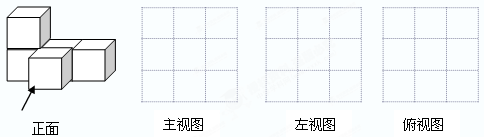
 如图,共有五个三角形,从位置看,哪一个是由下面这个三角形绕其直角顶点顺时针旋转180°得到的( )
如图,共有五个三角形,从位置看,哪一个是由下面这个三角形绕其直角顶点顺时针旋转180°得到的( )