题目内容
【题目】如图,OC平分∠AOB,CD⊥OA于D,CE⊥OB于E,连接DE,猜想DE与OC的位置关系?并说明理由. 
【答案】解:OC垂直平分DE,
∵OC平分∠AOB,
∴∠COD=∠COE,
又∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=90°,
在△COD和△COE中,
∵ 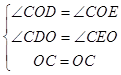 ,
,
∴△COD≌△COE(AAS),
∴OD=OE,OC=OE,
∴OC垂直平分DE
【解析】由OC平分∠AOB得∠COD=∠COE,由CD⊥OA、CE⊥OB知∠CDO=∠CEO=90°,从而证△COD≌△COE可得OD=OE,OC=OE,即可说明OC垂直平分DE.
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案,需要熟知定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

练习册系列答案
相关题目