题目内容
(2013•湖北)一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作;…;若在第n次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若AB=2,BC=6,则称矩形ABCD为2阶奇异矩形.

(1)判断与操作:
如图2,矩形ABCD长为5,宽为2,它是奇异矩形吗?如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.
(2)探究与计算:
已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出a的值.
(3)归纳与拓展:
已知矩形ABCD两邻边的长分别为b,c(b<c),且它是4阶奇异矩形,求b:c(直接写出结果).

(1)判断与操作:
如图2,矩形ABCD长为5,宽为2,它是奇异矩形吗?如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.
(2)探究与计算:
已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出a的值.
(3)归纳与拓展:
已知矩形ABCD两邻边的长分别为b,c(b<c),且它是4阶奇异矩形,求b:c(直接写出结果).
分析:(1)根据已知操作步骤画出即可;
(2)根据已知得出符合条件的有4种情况,画出图形即可;
(3)根据题意得出第1次操作前短边与长边之比为:
,
;
,
;
,
;
,
,最终得出长边和短边的比是1:2,即可进行操作后得出正方形.
(2)根据已知得出符合条件的有4种情况,画出图形即可;
(3)根据题意得出第1次操作前短边与长边之比为:
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 7 |
| 4 |
| 7 |
| 2 |
| 7 |
| 5 |
| 7 |
| 3 |
| 8 |
| 5 |
| 8 |
解答:解:(1)矩形ABCD是3阶奇异矩形,裁剪线的示意图如下:

(2)裁剪线的示意图如下:

(3)b:c的值为
,
,
,
,
,
,
,
,
规律如下:第4次操作前短边与长边之比为:
;
第3次操作前短边与长边之比为:
,
;
第2次操作前短边与长边之比为:
,
;
,
;
第1次操作前短边与长边之比为:
,
;
,
;
,
;
,
.

(2)裁剪线的示意图如下:

(3)b:c的值为
| 1 |
| 5 |
| 4 |
| 5 |
| 2 |
| 7 |
| 3 |
| 7 |
| 4 |
| 7 |
| 5 |
| 7 |
| 3 |
| 8 |
| 5 |
| 8 |
规律如下:第4次操作前短边与长边之比为:
| 1 |
| 2 |
第3次操作前短边与长边之比为:
| 1 |
| 3 |
| 2 |
| 3 |
第2次操作前短边与长边之比为:
| 1 |
| 4 |
| 3 |
| 4 |
| 2 |
| 5 |
| 3 |
| 5 |
第1次操作前短边与长边之比为:
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 7 |
| 4 |
| 7 |
| 2 |
| 7 |
| 5 |
| 7 |
| 3 |
| 8 |
| 5 |
| 8 |
点评:本题考查了矩形性质,正方形性质,寻找规律的应用,主要考查学生的变换能力和了解能力,注意:要进行分类讨论.

练习册系列答案
相关题目
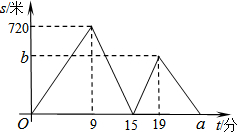 (2013•湖北)小文、小亮从学校出发到青少年宫参加书法比赛,小文步行一段时间后,小亮骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小文出发时间t(分)之间的函数关系如图所示.下列说法:①小亮先到达青少年宫;②小亮的速度是小文速度的2.5倍;③a=24;④b=480.其中正确的是( )
(2013•湖北)小文、小亮从学校出发到青少年宫参加书法比赛,小文步行一段时间后,小亮骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小文出发时间t(分)之间的函数关系如图所示.下列说法:①小亮先到达青少年宫;②小亮的速度是小文速度的2.5倍;③a=24;④b=480.其中正确的是( ) (2013•湖北)2013年5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系
(2013•湖北)2013年5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系