题目内容
设直角三角形的两条直角边长分别为a,b,斜边长为c.若a,b,c均为整数,且c=| 1 | 3 |
分析:先根据此三角形是直角三角形,利用勾股定理把原式化为(a-6)(b-6)=18,再根据a,b均为正整数,不妨设a<b,可得出关于a、b的二元一次方程,求出a、b、c的对应值即可.
解答:解:由勾股定理得,c2=a2+b2.
又∵c=
ab-(a+b),得c2=[
ab-(a+b)]2=
(ab)2-
ab(a+b)+(a+b)2.
即a2+b2=
(ab)2-
ab(a+b)+a2+2ab+b2.
整理得,ab-6(a+b)+18=0,即(a-6)(b-6)=18,
∵a,b均为正整数,不妨设a<b,
可得
或
或
,
可解出
或
或
,
∴满足条件的直角三角形有3个.
故答案为:3.
又∵c=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 2 |
| 3 |
即a2+b2=
| 1 |
| 9 |
| 2 |
| 3 |
整理得,ab-6(a+b)+18=0,即(a-6)(b-6)=18,
∵a,b均为正整数,不妨设a<b,
可得
|
|
|
可解出
|
|
|
∴满足条件的直角三角形有3个.
故答案为:3.
点评:本题考查的是非一次不定方程及勾股定理,解答此题的关键是先利用勾股定理把原式化为两个因式积的形式,再根据a,b均为正整数进行解答.

练习册系列答案
相关题目

 不妨设
不妨设 ,三条边上的对应高分别为
,三条边上的对应高分别为 ,内接正方形的边长分别为
,内接正方形的边长分别为 .若你对本小题证明有困难,可直接用“
.若你对本小题证明有困难,可直接用“ ”这个结论,但在证明正确的情况下扣1分).
”这个结论,但在证明正确的情况下扣1分).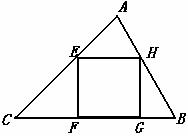
 形的内接正方形的有关问题进行了探讨:
形的内接正方形的有关问题进行了探讨: 同学的结果正确吗?若不正确,请举出一个反例并通过计算给予说明,若正确,请给出证明;
同学的结果正确吗?若不正确,请举出一个反例并通过计算给予说明,若正确,请给出证明; C的三条边分别为
C的三条边分别为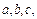 不妨设
不妨设 ,三条边上的对应高分别为
,三条边上的对应高分别为 ,内接正方形的边长分别为
,内接正方形的边长分别为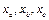 .若你对本小题证明有困难,可直接用
.若你对本小题证明有困难,可直接用 “
“ ”这个结论,但在证明正确的情况下扣1分).
”这个结论,但在证明正确的情况下扣1分).
 不妨设
不妨设 ,三条边上的对应高分别为
,三条边上的对应高分别为 ,内接正方形的边长分别为
,内接正方形的边长分别为 .若你对本小题证明有困难,可直接用“
.若你对本小题证明有困难,可直接用“ ”这个结论,但在证明正确的情况下扣1分).
”这个结论,但在证明正确的情况下扣1分).
 ”这个结论,但在证明正确的情况下扣1分)。
”这个结论,但在证明正确的情况下扣1分)。 