��Ŀ����
��ͼ����è����Ĺ����У��������ų����ε�����A��B��D��·���Ӵܣ�èͬʱ����¥��A��C��Dȥ�������è��D��ס�������߶�CD��0.6�ף�
��1����¥��A��C���ܳ�Ϊx�ף�è�������õ�ʱ��Ϊt�룮������ұߵı���
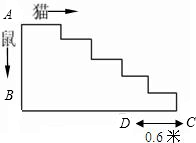
��2����֪������ٶ���è�ٶȵ�
�����ܲ������á��ٶȡ���һ�������йصĴ���ʽ����������
��1����¥��A��C���ܳ�Ϊx�ף�è�������õ�ʱ��Ϊt�룮������ұߵı���

| ¥��A-C���ܳ�Ϊ | x�� |
| AB+BC�ij�Ϊ | |
| è����·��Ϊ | |
| �����Ӵܵ�·��Ϊ | |
| ��è�������õ�ʱ��Ϊ | t�� |
| è���ٶ��� | |
| ������ٶ��� |
| 11 |
| 14 |
��1����¥�ݵĸ����߶ν���ƽ�ƣ��ɵ�AB+BC=¥��A��C���ܳ�=x��
è���·��֮��Ϊ=¥��A��C���ܳ�+�߶�CD��=x+0.6��
�����Ӵܵ�·��=AB+BC-�߶�CD��=x-0.6��
è���ٶ�=è��·�̡�è�õ�ʱ��=
��
������ٶ�=�����ߵ�·�̡��������ܵ�ʱ��=
��
�ʴ�Ϊ��x�ף���x+0.6���ף���x-0.6���ף�
��/�룬
��/����
��2����������ٶ���è�ٶȵ�
��è���ٶ�=
��������ٶ�=
��
��
=
��
��
è���·��֮��Ϊ=¥��A��C���ܳ�+�߶�CD��=x+0.6��
�����Ӵܵ�·��=AB+BC-�߶�CD��=x-0.6��
è���ٶ�=è��·�̡�è�õ�ʱ��=
| x+0.6 |
| t |
������ٶ�=�����ߵ�·�̡��������ܵ�ʱ��=
| x-0.6 |
| t |
�ʴ�Ϊ��x�ף���x+0.6���ף���x-0.6���ף�
| x+0.6 |
| t |
| x-0.6 |
| t |
��2����������ٶ���è�ٶȵ�
| 11 |
| 14 |
| x+0.6 |
| t |
| x-0.6 |
| t |
��
| x-0.6 |
| t |
| 11 |
| 14 |
| x+0.6 |
| t |

��ϰ��ϵ�д�
�����Ŀ