题目内容
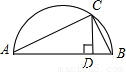
如图AB为半圆的直径，C为半圆上的一点，CD⊥AB于D，连接AC，BC，则与∠ACD互余的角有（ ）
A．1个
B．2个
C．3个
D．4个
【答案】分析：已知了CD⊥AB，在Rt△ACD中可找出∠ACD的余角为∠A；由于AB是半圆的直径，根据圆周角定理可知：∠ACB=90°，由此可得出∠ACD的余角为∠BCD；因此∠ACD的余角共有2个．
解答：解：∵AB是半圆的直径
∴∠ACB=90°
∴∠ACD+∠BCD=90°
∵CD⊥AB
∴∠ADC=∠BDC=90°
∴∠A+∠ACD=90°
即∠ACD的余角有两个，为：∠A和∠BCD．
故选B．
点评：解答本题的关键是掌握圆周角定理的推论以及直角三角形的两个锐角互余的性质．
解答：解：∵AB是半圆的直径
∴∠ACB=90°
∴∠ACD+∠BCD=90°
∵CD⊥AB
∴∠ADC=∠BDC=90°
∴∠A+∠ACD=90°
即∠ACD的余角有两个，为：∠A和∠BCD．
故选B．
点评：解答本题的关键是掌握圆周角定理的推论以及直角三角形的两个锐角互余的性质．
练习册系列答案
备战中考寒假系列答案
相关题目
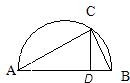9、如图AB为半圆的直径，C为半圆上的一点，CD⊥AB于D，连接AC，BC，则与∠ACD互余的角有（ ）
