Question

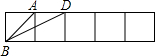（2012•洪山区模拟）正方形网格中，△ABD如图放置，其顶点A、B、D都在格点上．
（1）在格点上，找点C，使△DCB∽△ABD，请画出△DCB（仅画图即可，不必说明理由）
（2）求cos∠ABD的值．

Answer 1

分析：（1）根据相似三角形的判定方法以及正方形的性质即可画出图形；
（2）在Rt△DEC中，利用勾股定理求出DC的长，再求出cos∠DCB的值，最后根据△DCB∽△ABD，得出∠ABD=∠DCB，即可求出答案．

解答：解：（1）画图如下：


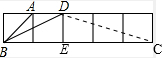
（2）在Rt△DEC中，∠DEC=90°，
∵DE=1，EC=3，
∴DC=

12+32

=

10

，
∴cos∠DCB=

EC

DC

=

3

10

=

3 10

10

，
∵△DCB∽△ABD，
∴∠ABD=∠DCB，
∴cos∠ABD=cos∠DCB=

3 10

10

．

点评：此题考查了作图-相似变化，用到的知识点是相似三角形的判定与性质，利用图形得出各边长度，再利用相似三角形的性质得出是解题关键．