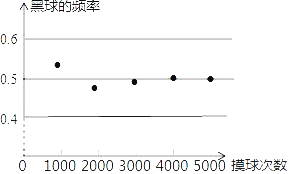
��Ŀ����
����Ŀ����ͼ������ƽ��ֱ������ϵxOy�У���һ������ֱ��������AOB����OAB=90����ֱ�DZ�AO��x���ϣ���AO=1����Rt��AOB��ԭ��O˳ʱ����ת90���õ�����ֱ��������A1OB1����A1O=2AO���ٽ�Rt��A1OB1��ԭ��O˳ʱ����ת90���õ�����������A2OB2����A2O=2A1O�������˹��ɣ��õ�����ֱ��������A2019OB2019�����A2019������Ϊ_______ ��

���𰸡���0��22019��
��������
��������ó���A�ı仯���ɣ������ɵõ���A2019��λ�ü�OA2019�ij������ɵô𰸣�
��AO=1����Rt��AOB��ԭ��O˳ʱ����ת90���õ�����ֱ��������A1OB1����A1O=2AO���ٽ�Rt��A1OB1��ԭ��O˳ʱ����ת90���õ�����������A2OB2����A2O=2A1O�������˹��ɣ�
��ÿ4��ѭ��һ�ܣ�A1��0����2����A2����4��0����A3��0��8����A4��16��0��������
��2019��4=504����3��
���A2019��A3ͬ��y�������ᣬ
��-2=-21����4=��22��8=23��16=24��������
��OA2019=22019��
���A2019��������0��22019����
�ʴ�Ϊ����0��22019��

��ϰ��ϵ�д�
�����Ŀ