��Ŀ����
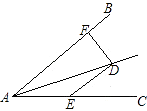
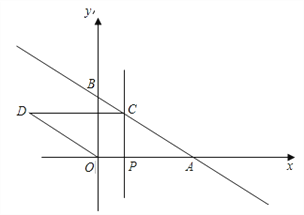
����Ŀ����ͼ����ֱ֪��y=kx+b��x�ύ��A��8��0������y�ύ��B��0��6������P��x���������ϵ�һ���㣬����P��PC��x�ᣬ��ֱ��AB�ڵ�C����OA��ACΪ�߹�����OACD�����P�ĺ�����Ϊm��
��1����ֱ��AB�ĺ�������ʽ��
��2�����ı���OACDǡ�����Σ������m��ֵ��
��3���ڣ�2���������£�y������Ƿ���ڵ�Q������CQ��ʹ�á�OQC+��ODC=180�㣮�����ڣ�ֱ��д�����з��������ĵ�Q�����꣬�������ڣ���˵�����ɣ�
���𰸡���1��y=![]() ����2��
����2��![]() ��
��![]() ����3��Q1(0��
����3��Q1(0�� ![]() ); Q,2(0��-24) ;Q,3(0��
); Q,2(0��-24) ;Q,3(0�� ![]() ).
).
����������1���ѵ�A��8��0����B��0��6������ֱ��y=kx+b�ⷽ�̿ɵã�
��2���������ε����ʵõ�AC=2���ɵ�C��m�� ![]() m+1���õ�AP=|2-m|��CP=
m+1���õ�AP=|2-m|��CP=![]() +1�����ù��ɶ����з��̿ɵã�
+1�����ù��ɶ����з��̿ɵã�
��3�����ı���OACD�����Σ��õ��Խ���ȣ���D=��OAC������ʱQ��y���ϣ������ı���ACQO�ĶԽǻ������õ�CQ��AC�����ֱ��CQ�Ľ���ʽ�����Q�������.
�⣺��1���ѵ�A��8��0����B��0��6������ֱ��y=kx+b��
�ɵ�![]() �����
�����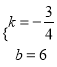 ��
��
��ֱ��AB�ĺ�������ʽΪy=![]() x+6
x+6
(2)�ٵ�m��OA��
��OA=AC
��10- ![]() =8
=8
���m=![]()
�ڵ�m��OA�ӳ�����
��OA=AC
��![]() -10=8
-10=8
���m=![]()
Q1(0�� ![]() ); Q,2(0��-24) ;Q,3(0��
); Q,2(0��-24) ;Q,3(0�� ![]() ).
).
���㾦������Ϊһ�κ�����Ӧ�ã��漰����ϵ���������ε����ʡ����ɶ���������˼���֪ʶ���ڣ�1����ע�����ϵ����Ӧ�ò��裬�ڣ�2�����������ε����ʵõ�C�������ǽ���Ĺؼ����ڣ�3�������QC��AB�ǽ���Ĺؼ�.���⿼��֪ʶ��࣬�ۺ��Խ�ǿ���Ѷ�����.