题目内容
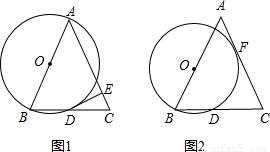
如图，点D在等腰△ABC底边BC上，且AB=BD，E是AC上一点，且AE=AD，∠DAE=30°，则∠B=（ ）分析：根据三角形内角和定理和等腰三角形的性质，可得关于∠B的方程，解方程求解即可．
解答：解：∠B+∠C+∠BAD+∠DAE=180°
∵AB=BD，
∴∠BAD=∠BDA．
∵AE=AD，
∴∠ADE=∠AED，
∵∠DAE=30°，
∴∠B+∠B+
（180°-∠B）+30°=180°，
∴∠B=40°．
故选B．
∵AB=BD，
∴∠BAD=∠BDA．
∵AE=AD，
∴∠ADE=∠AED，
∵∠DAE=30°，
∴∠B+∠B+
| 1 |
| 2 |
∴∠B=40°．
故选B．
点评：考查了等腰三角形的性质：等腰三角形的两个底角相等．
练习册系列答案
同步练习强化拓展系列答案
相关题目
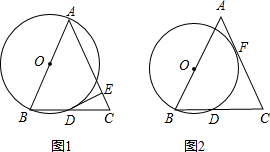若S△ABC=25，AB=10，点O移动到何处⊙O与AC相切于点F？
若S△ABC=25，AB=10，点O移动到何处⊙O与AC相切于点F？
如图，点D在等腰△ABC底边BC上，且AB=BD，E是AC上一点，且AE=AD，∠DAE=30°，则∠B=