题目内容
【题目】已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.
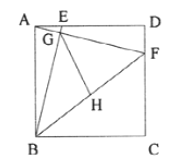
【答案】5
【解析】
根据正方形的四条边都相等可得AB=AD,每一个角都是直角可得∠BAE=∠D=90°;然后利用“边角边”证明△ABE≌△DAF得∠ABE=∠DAF,进一步得∠AGE=∠BGF=90°,从而知GH=![]() BF,利用勾股定理求出BF的长即可得出答案.
BF,利用勾股定理求出BF的长即可得出答案.
∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在△ABE和△DAF中,∵AB=AD,∠BAE=∠D,AE=DF,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=![]() BF,
BF,
∵BC=8,CF=CD-DF=8-2=6,
∴BF=![]() =10,
=10,
∴GH=![]() BF=5.
BF=5.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
【题目】在一个不透明的袋子中装有仅颜色不同的![]() 个小球,其中红球
个小球,其中红球![]() 个,白球
个,白球![]() 个.
个.
(1)先从袋子中取出![]() 个红球(
个红球(![]() 且
且![]() 为正整数),再从袋子中随机摸
为正整数),再从袋子中随机摸![]() 个小球,将“摸出白球”记为事件A,请完成下面表格:
个小球,将“摸出白球”记为事件A,请完成下面表格:
事件 | 必然事件 | 随机事件 |
|
(2)先从袋子中取出![]() 个红球,再放入
个红球,再放入![]() 个一样的白球并掘匀,随机摸出
个一样的白球并掘匀,随机摸出![]() 个白球的频率在
个白球的频率在![]() 附近摆动,求
附近摆动,求![]() 的值.
的值.