题目内容
若m=
，
（1）求m的值；
（2）求（m-1）2的值；
（3）求m5-2m4-2013m3的值．
| 2 013 | ||
|
（1）求m的值；
（2）求（m-1）2的值；
（3）求m5-2m4-2013m3的值．
考点：二次根式的化简求值
专题：
分析：（1）直接分子分母乘（
+1）化简即可；
（2）直接代入（1）中的求得结果；
（3）把原式分解因式，利用（2）的结果解决问题．
| 2014 |
（2）直接代入（1）中的求得结果；
（3）把原式分解因式，利用（2）的结果解决问题．
解答：解：（1）m=
=
+1；
（2）（m-1）2=（
+1-1）2=2014；
（3）m5-2m4-2013m3=m3（m2-2m-2013）=m3[（m-1）2-2014]=m3[2014-2014]=0．
| 2 013 | ||
|
| 2014 |
（2）（m-1）2=（
| 2014 |
（3）m5-2m4-2013m3=m3（m2-2m-2013）=m3[（m-1）2-2014]=m3[2014-2014]=0．
点评：此题考查二次根式的化简，完全平方公式的运用，以及整体代入的思想渗透．
练习册系列答案
相关题目
五张完全相同的卡片上，分别画有圆、矩形、等边三角形、平行四边形、等腰梯形，现从中任意抽取一张，卡片上画的恰好是中心对称图形的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知3是关于x的方程2x-a=1的解，则a的值为（ ）
| A、-5 | B、5 | C、7 | D、-7 |
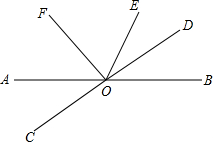如图，直线AB、CD相交于点O，∠DOE=∠BOD，OF平分∠AOE，若∠BOD=28°
在四边形ABCD中，AD∥BC，且AD=8cm，BC=6cm，P、Q分别从A、C同时出发，P以1cm/s的速度由A向D运动，Q以2cm/s的速度由C出发向B运动，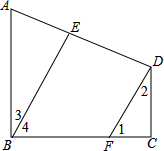
AB⊥BC，∠1+∠2=90°，∠2=∠3．BE与DF平行吗？为什么？