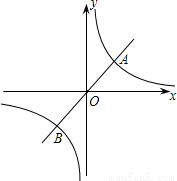
题目内容
(2006•永春县)如图,正比例函数y=kx的图象与反比例函数y= 的图象相交于A、B两点,且A的坐标为(1,1).
的图象相交于A、B两点,且A的坐标为(1,1).(1)求正比例函数的解析式;
(2)已知M,N是y轴上的点,若四边形AMBN是矩形,求M、N的坐标.

【答案】分析:(1)把(1,1)代入函数式y=kx中,可求出函数解析式;
(2)解两个函数式组成的方程组,可求出B的坐标(-1,-1),再设Y轴正半轴上的点M坐标为(0,y),那么设负半轴上的坐标为(0,-y).根据勾股定理,以及两点之间的距离公式,可求出y1= ,y2=-
,y2=- ,于是M点坐标是(0,
,于是M点坐标是(0, ),N点坐标是(0,-
),N点坐标是(0,- ).
).
解答:解:(1)把(1,1)代入y=kx中,得,1=1×k,即k=1
∴正比例函数的解析式为:y=x;
(2)解 ,可得
,可得 ;
; ,即B点坐标是(-1,-1).
,即B点坐标是(-1,-1).
设y轴正半轴上M坐标是(0,y),负半轴上N点坐标为(0,-y).
∴根据勾股定理,得(y+1)2+1+(-y-1)2+1=(1+1)2+(1+1)2,解得,y1= ,y2=-
,y2=- .
.
∴M点的坐标为(0, ),N点的坐标为(0,-
),N点的坐标为(0,- ).
).
点评:本题利用了待定系数法求函数解析式以及利用方程组求两个函数的交点,两点之间距离公式、勾股定理等知识.
(2)解两个函数式组成的方程组,可求出B的坐标(-1,-1),再设Y轴正半轴上的点M坐标为(0,y),那么设负半轴上的坐标为(0,-y).根据勾股定理,以及两点之间的距离公式,可求出y1=
 ,y2=-
,y2=- ,于是M点坐标是(0,
,于是M点坐标是(0, ),N点坐标是(0,-
),N点坐标是(0,- ).
).解答:解:(1)把(1,1)代入y=kx中,得,1=1×k,即k=1
∴正比例函数的解析式为:y=x;
(2)解
 ,可得
,可得 ;
; ,即B点坐标是(-1,-1).
,即B点坐标是(-1,-1).设y轴正半轴上M坐标是(0,y),负半轴上N点坐标为(0,-y).
∴根据勾股定理,得(y+1)2+1+(-y-1)2+1=(1+1)2+(1+1)2,解得,y1=
 ,y2=-
,y2=- .
.∴M点的坐标为(0,
 ),N点的坐标为(0,-
),N点的坐标为(0,- ).
).点评:本题利用了待定系数法求函数解析式以及利用方程组求两个函数的交点,两点之间距离公式、勾股定理等知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的图象相交于A、B两点,且A的坐标为(1,1).
的图象相交于A、B两点,且A的坐标为(1,1).