题目内容
 如图所示,某海关缉私巡逻艇在海上执行巡逻任务时,发现在其所处位置O点的正北方向10海里的A点有一涉嫌走私船只,正以
如图所示,某海关缉私巡逻艇在海上执行巡逻任务时,发现在其所处位置O点的正北方向10海里的A点有一涉嫌走私船只,正以 海里/时的速度向正东方向航行,为了迅速实施检查,巡逻艇调整好航向,以20海里/时的速度追赶,在涉嫌走私船只不改变航向和航速的前提下,问:
海里/时的速度向正东方向航行,为了迅速实施检查,巡逻艇调整好航向,以20海里/时的速度追赶,在涉嫌走私船只不改变航向和航速的前提下,问:
(1)需要几小时才能追上?(点B为追上时的位置)
(2)确定巡逻艇的追赶方向.
解:(1)设需要t小时才能追上,
则:AB=10 t,OB=20t.
t,OB=20t.
在Rt△AOB中:OB2=OA2+AB2,即:(20t)2=102+(10 t)2,
t)2,
解得:t=±1,t=-1(不合题意,舍去).
故需要1小时才能追上;
(2)在Rt△AOB中
∵sin∠AOB=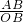 =
= =
= ,
,
∴∠AOB=60°
即巡逻艇的追赶方向为北偏东60°.
分析:(1)在Rt△AOB中,设需要t小时才能追上,根据三角函数就可以得到关于t的方程,解方程就可以求出t的值.
(2)在Rt△AOB中,已知三边,就可以求出三角函数值,就可以求出角的度数.
点评:考查了勾股定理的应用,在直角三角形中,已知两边的长就可以求出第三边与两个锐角.
则:AB=10
 t,OB=20t.
t,OB=20t.在Rt△AOB中:OB2=OA2+AB2,即:(20t)2=102+(10
 t)2,
t)2,解得:t=±1,t=-1(不合题意,舍去).
故需要1小时才能追上;
(2)在Rt△AOB中
∵sin∠AOB=
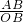 =
= =
= ,
,∴∠AOB=60°
即巡逻艇的追赶方向为北偏东60°.
分析:(1)在Rt△AOB中,设需要t小时才能追上,根据三角函数就可以得到关于t的方程,解方程就可以求出t的值.
(2)在Rt△AOB中,已知三边,就可以求出三角函数值,就可以求出角的度数.
点评:考查了勾股定理的应用,在直角三角形中,已知两边的长就可以求出第三边与两个锐角.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 如图所示,某海关缉私巡逻艇在海上执行巡逻任务时,发现在其所处位置O点的正北方向10海里的A点有一涉嫌走私船只,正以
如图所示,某海关缉私巡逻艇在海上执行巡逻任务时,发现在其所处位置O点的正北方向10海里的A点有一涉嫌走私船只,正以