Question

如图，AB是⊙O的直径，AD是弦，点E是弧BD上一点，EF⊥AD于点F，且EF是⊙O的切线．
（1）求证：弧DE=弧BE；
（2）连接BE，若tan∠DAB=

12

5

，求tan∠B的值．

Answer 1

分析：（1）如图，连接OD、OE．欲证明弧DE=弧BE，只需证明∠5=∠4；
（2）连接BD，AE，根据直角△ABD中，tan∠DAB=

BD

AD

=

12

5

，可以设BD=12a，则AD=5a，根据弧DE=弧BE，可以得到OE垂直平分BD，则在直角△OMB中，利用勾股定理即可求得OM，然后在直角△BEM中，利用勾股定理求得BE的长，在直角△ABE中利用勾股定理求得AE的长，然后根据正切函数的定义即可求解．

解答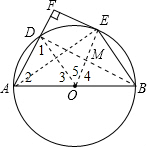：解：（1）如图，连接OD、OE．
∵OA=OD，
∴∠1=∠2．
∵AB是⊙O的直径，EF是⊙O的切线，
∴OE⊥EF．
又∵EF⊥AD于点F，
∴AF∥OE，
∴∠1=∠5，∠2=∠4，
∴∠5=∠4，
∴弧DE=弧BE；

（2）连接BD，AE，
∵AB是圆的直径，
∴∠ADB=90°，
∵直角△ABD中，tan∠DAB=

BD

AD

=

12

5

，
∴设BD=12a，则AD=5a，
则直径AB=

AD2+BD2

=13a，
∵弧DE=弧BE；
∴BM=

1

2

BD=6a，OE⊥BD，
∴在直角△ONM中，OM=

OB2-BM2

=

(6.5a)2-(6a)2

=

5

2

a，
∴ME=OE-OM=6.5a-

5

2

a=4a，
在直角△BEM中，BE=

ME2+MB2

=

(4a)2+(6a)2

=2

13

a，
在直角△ABE中，AE=

AB2-BE2

=

(13a)2-52a2

=

117

a，
∴tan∠B=

AE

BE

=

117 a

2 13 a

=

3

2

．

点评：本题考查了切线的性质，圆周角定理以及勾股定理，三角函数，正确理解三角函数的定义，作出辅助线是关键．