题目内容
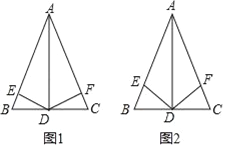
【题目】(1)如图1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于点E,DF⊥AC于点F.证明:DE=DF.
(2)如图2,在△ABC中,AB=AC,AD⊥BC,DE和DF分别平分∠ADB和∠ADC,求证:DE=DF.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)在△ABC中,AB=AC,AD⊥BC,根据等腰三角形三线合一的性质可得∠BAD=∠CAD,又因DE⊥AB,DF⊥AC,根据角平分线的性质定理即可证得DE=DF;(2)在△ABC中,AB=AC,AD⊥BC,根据等腰三角形三线合一的性质可得∠BAD=∠CAD,∠ABD=∠CDA=90°,又因DE平分∠ADB,DF平分和∠ADC,可得∠ADE=∠ADF=45°,利用ASA证得△AED≌△AFD,根据全等三角形等的性质即可得结论.
试题解析:
(1)证明:∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
∵DE⊥AB,DF⊥AC
∴DE=DF;
(2)证明:∵AB=AC,AD⊥BC
∴∠BAD=∠CAD,
∵DE平分∠ADB,DF平分和∠ADC,
∴∠ADE=∠ADF=45°,
在△AED和△AFD中,
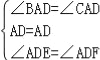 ,
,
∴△AED≌△AFD(ASA),
∴DE=DF.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目

