题目内容
如图,AB是半圆的直径,AC为半圆的切线,AC=AB、在半圆上任取一点D,作DE⊥CD,交直线AB于点F,BF⊥AB,交线段AD的延长线于点F.(1)设
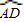 是x°的弧,并要使点E在线段BA的延长线上,则x的取值范围是______;
是x°的弧,并要使点E在线段BA的延长线上,则x的取值范围是______;(2)不论D点取在半圆什么位置,图中除AB=AC外,还有两条线段一定相等,指出这两条相等的线段,并予证明.
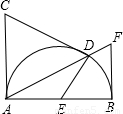
【答案】分析:可利用特殊位置即对运动变化趋势的观察,从而将不可能的情况排除,或从正面得到BE=BF的猜想.
解答:解:(1)0<x<90,
(2)连接BD,可证△BDF∽△ADB,得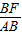 =
=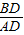 ,
,
∵∠DBE=∠DAC,
∴∠BDE=∠ADC=90°-∠ADE,
∴△BDE∽△ADC,
∴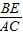 =
=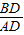 ,
,
∴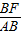 =
=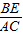 ,
,
∴BE=BF.
点评:本题考查了相似三角形的判定和性质以及切线的性质,是一道综合题,有一定的难度.
解答:解:(1)0<x<90,
(2)连接BD,可证△BDF∽△ADB,得
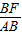 =
=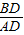 ,
,∵∠DBE=∠DAC,
∴∠BDE=∠ADC=90°-∠ADE,
∴△BDE∽△ADC,
∴
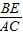 =
=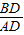 ,
,∴
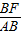 =
=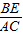 ,
,∴BE=BF.
点评:本题考查了相似三角形的判定和性质以及切线的性质,是一道综合题,有一定的难度.

练习册系列答案
相关题目
 道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)
道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)


