题目内容
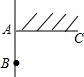一束阳光射在窗子AB上，此时光与水平线夹角为30°，若窗高AB=1.8米，要想将光线全部遮挡住，不能射到窗子AB上，则挡板AC（垂直于AB）的长最少应为（ ）分析：根据已知作出辅助线，再利用
=tan30°得出AC的长即可．
| AB |
| AC |
解答：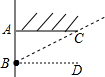
解：如图所示：设光线为CB，作DB⊥AB于点B，
∵光与水平线夹角为30°，
∴∠CBD=30°，
∵AC∥BD，
∴∠ACB=30°，
∵AB=1.8米，
∴
=tan30°，
∴AC=
=
=1.8
=
．
故选：A．
解：如图所示：设光线为CB，作DB⊥AB于点B，∵光与水平线夹角为30°，
∴∠CBD=30°，
∵AC∥BD，
∴∠ACB=30°，
∵AB=1.8米，
∴
| AB |
| AC |
∴AC=
| AB |
| tan30° |
| 1.8 | ||||
|
| 3 |
9
| ||
| 5 |
故选：A．
点评：此题主要考查了解直角三角形的应用，利用锐角三角函数关系得出
=tan30°是解题关键．
| AB |
| AC |
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目