��Ŀ����
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬��O��������OC��ʹ��AOC����BOC��1��2����һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·���
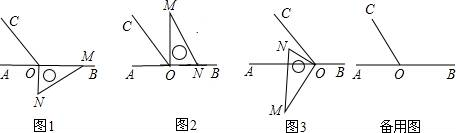
��1����ͼ1�е����ǰ��Ƶ�O����ʱ�뷽����ת��ͼ2��λ�ã�ʹ��ON��������OB�ϣ���ʱ���ǰ���ת�ĽǶ�Ϊ�� ���ȣ�
��2��������ͼ2�е����ǰ��Ƶ�O����ʱ�뷽����ת��ͼ3��λ�ã�ʹ��ON�ڡ�AOC���ڲ�����̽����AOM���NOC֮������ʲô������ϵ����˵�����ɣ�
��3��������ֱ�����ǰ��ͼ1��ʱ����ת��ͼ3��λ�õĹ����У������ǰ��Ƶ�O��15��ÿ����ٶ���ת����ֱ�����ǰ��ֱ�DZ�ON����ֱ��ǡ��ƽ�֡�AOCʱ�����ʱ���ǰ��Ƶ�O���˶�ʱ��t��ֵ��
���𰸡���1��90 ��2���𰸼����� ��3��4���16��
��������
��1��������ת������֪����ת���ǡ�MON��
��2����ͼ3������ƽ�ǵĶ��壬�����֪��������AOC����BOC��1��2����á�AOC��60�㣻Ȼ����ֱ�ǵ����ʡ�ͼ�н���Ǽ��������ϵ��֪��AOM����NOC��30�㣻
��3����Ҫ�������ۣ���������ֱ�DZ�ON�ڡ�AOC�ⲿʱ����ת����60�㣻��������ֱ�DZ�ON�ڡ�AOC�ڲ�ʱ����ת����240��
�⣺��1������ת������֪����ת�ǡ�MON��90�㣮
�ʴ��ǣ�90��
��2����ͼ3����AOM����NOC��30�㣮
���AOC�������ɡ�AOC����BOC��1��2�ɵ�
��BOC��2����
�ߡ�AOC+��BOC��180�㣬
���+2����180�㣮
��� ����60�㣮
����AOC��60�㣮
���AON+��NOC��60�㣮��
�ߡ�MON��90�㣬
���AOM+��AON��90�㣮��
�ɢک��٣��á�AOM����NOC��30�㣻
��3����������ͼ4����ֱ�DZ�ON�ڡ�AOC�ⲿʱ��
��ODƽ�֡�AOC���ɵá�BON��30�㣮
������ǰ��Ƶ�O��ʱ����ת60�㣮
��ʱ���ǰ���˶�ʱ��Ϊ��
t��60���15�㣽4���룩��
��������ͼ5����ֱ�DZ�ON�ڡ�AOC�ڲ�ʱ��
��ONƽ�֡�AOC���ɵá�CON��30�㣮
������ǰ��Ƶ�O��ʱ����ת240�㣮
��ʱ���ǰ���˶�ʱ��Ϊ��
t��240���15�㣽16���룩��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�