题目内容
已知a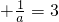
，求
（1）
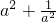的值；
（2）a3-a2-5a+2010的值．
解：（1）∵a，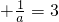
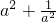∴=（a+
）2-2=32-2=7
（2）a3-a2-5a+2010
=a3+a-a2-6a+2010
=a2（a+）-a2-6a+2010
=3a2-a2-6a+2010
=2a2-6a+2010
=2a2+2-6a+2008
=2a（a+）-6a+2008
=6a-6a+2008
=2008
分析：（1）将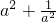变形为（a+）2-2即可得到答案．
（2）将a3-a2-5a+2010变形为a2（a+）-a2-6a+2010代入a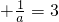后进一步得到3a2-a2-6a+2010，再进一步变形后继续代入即可求得答案．
点评：本题考查了因式分解的应用及完全平方公式，解题的关键是熟悉因式分解的方法并正确的变形．
，∴
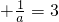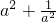=（a+）2-2=32-2=7（2）a3-a2-5a+2010
=a3+a-a2-6a+2010
=a2（a+
）-a2-6a+2010=3a2-a2-6a+2010
=2a2-6a+2010
=2a2+2-6a+2008
=2a（a+
）-6a+2008=6a-6a+2008
=2008
分析：（1）将
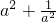变形为（a+）2-2即可得到答案．（2）将a3-a2-5a+2010变形为a2（a+
）-a2-6a+2010代入a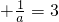后进一步得到3a2-a2-6a+2010，再进一步变形后继续代入即可求得答案．点评：本题考查了因式分解的应用及完全平方公式，解题的关键是熟悉因式分解的方法并正确的变形．
练习册系列答案
名校课堂系列答案
相关题目
，求x2+5x﹣6的值．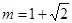
，
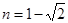，求（1）
,
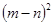的值；（2）
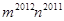的值；（3）
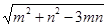的值.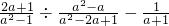
（再取一个你认为合适的a的值代入求值）
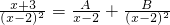，求A、B的值．
．
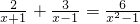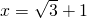，求x2-x+1的值．
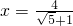，求x2+5x-6的值．