题目内容
【题目】某海域有A，B，C三艘船正在捕鱼作业，C船突然出现故障，向A，B两船发出紧急求救信号，此时B船位于A船的北偏西72°方向，距A船24海里的海域，C船位于A船的北偏东33°方向，同时又位于B船的北偏东78°方向．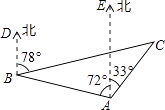
（1）求∠ABC的度数；
（2）A船以每小时30海里的速度前去救援，问多长时间能到出事地点．（结果精确到0.01小时）．
（参考数据： 
≈1.414， 
≈1.732）
【答案】
（1）解：∵BD∥AE，
∴∠DBA+∠BAE=180°，
∴∠DBA=180°﹣72°=108°，
∴∠ABC=108°﹣78°=30°
（2）解：作AH⊥BC，垂足为H，
∴∠C=180°﹣72°﹣33°﹣30°=45°，
∵∠ABC=30°，
∴AH= 
AB=12，
∵sinC= 
，
∴AC= 
= 
=12 
．
则A到出事地点的时间是： 
≈ 
≈0.57小时．
答：约0.57小时能到达出事地点．
【解析】（1）利用平行线的性质：同旁内角互补可求出；（2）通过作垂线，作AH⊥BC把特殊角 ，放在直角三角形中，利用三角函数联系边与边，求出AC.
练习册系列答案
相关题目
【题目】老李上周五以收盘价每股8元买入某公司股票10000股，下表为本周内每日该股票的涨跌情况（单位：元）：
星期 | 一 | 二 | 三 | 四 | 五 |
股票涨跌 | -0.1 | 0.35 | -0.15 | -0.4 | 0.5 |
（1）星期三的收盘价比老李的买入价涨或跌了多少元？
（2）本周内该股票的最高收盘价出现在星期几？是多少元？
（3）已知老李买进股票时要付成交额1‰的手续费，卖出时还需要付成交额的1‰的印花税和1‰的手续费．如果老李在星期五收盘前将该股票全部卖出，则他的收益情况如何？
