Question

【题目】如图，已知直线y=﹣x+2分别与x轴，y轴交于A，B两点，与双曲线y= 交于E，F两点，若AB=2EF，则k的值是（ ）

A.﹣1
B.1
C.
D.

Answer 1

【答案】D
【解析】解：作FH⊥x轴，EC⊥y轴，FH与EC交于D，如图，

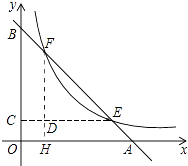
A点坐标为（2，0），B点坐标为（0，2），OA=OB，

∴△AOB为等腰直角三角形，

∴AB= OA=2 ，

∴EF= AB= ，

∴△DEF为等腰直角三角形，

∴FD=DE= EF=1，

设F点横坐标为t，代入y=﹣x+2，则纵坐标是﹣t+2，则F的坐标是：（t，﹣t+2），E点坐标为（t+1，﹣t+1），

∴t（﹣t+2）=（t+1）（﹣t+1），解得t= ，

∴E点坐标为（ ， ），

∴k= × = ．

所以答案是：D．