题目内容
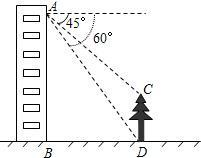如图，小芸在自家楼房的窗户A处，测量楼前的一棵树CD的高．现测得树顶C处的俯角为45°，树底D处的俯角为60°，楼底到大树的距离BD为20米．请你帮助小芸计算树的高度（精确到0.1米）．
分析：过点A作AE∥BD交DC的延长线于点E．则在图中得到两个直角三角形，利用三角函数定义分别计算出ED和EC，求差即可．
解答：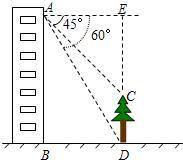
解：过点A作AE∥BD交DC的延长线于点E．
则∠AEC=∠BDC=90度．
∵∠EAC=45°，AE=BD=20米，
∴EC=20米．
∵tan∠ADB=tan∠EAD=
，
∴AB=20•tan60°=20
（米），
CD=ED-EC=AB-EC=20
-20≈14.6（米）．
答：树高约为14.6米．
解：过点A作AE∥BD交DC的延长线于点E．则∠AEC=∠BDC=90度．
∵∠EAC=45°，AE=BD=20米，
∴EC=20米．
∵tan∠ADB=tan∠EAD=
| AB |
| BD |
∴AB=20•tan60°=20
| 3 |
CD=ED-EC=AB-EC=20
| 3 |
答：树高约为14.6米．
点评：本题要求学生借助俯角构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
相关题目
