题目内容
 (2012•温州三模)如图,在正方形ABCD中,点E、F、G、H均在其内部,且DE=EF=FG=GH=HB=2,∠E=∠F=∠G=∠H=60°,则正方形ABCD的边长AB=
(2012•温州三模)如图,在正方形ABCD中,点E、F、G、H均在其内部,且DE=EF=FG=GH=HB=2,∠E=∠F=∠G=∠H=60°,则正方形ABCD的边长AB=| 14 |
| 14 |
分析:连接DH、BE,可以证明四边形DHBE是平行四边形,连接BD、EH,设交点为O,根据等边三角形的性质可得OE垂直平分FG,从而得到△ODE是直角三角形,然后求出OE的长度,再利用勾股定理列式计算求出OD的长度,再根据平行四边形的对角线互相平分可得BD=2OD,然后跟正方形的边长等于对角线的
求解即可.
| ||
| 2 |
解答: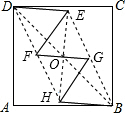 解:如图,连接DH、BE,
解:如图,连接DH、BE,
∵∠E=∠F=∠G=∠H=60°,
∴DE∥FG∥HB,
∵DE=EF=FG=GH=HB=2,
∴四边形DHBE是平行四边形,
连接BD、EH,设交点为O,
则OE垂直平分FG,
∴OE⊥DE,
∵EF=FG=2,
∴OE=2×
=
,
在Rt△ODE中,OD=
=
=
,
∴BD=2OD=2
,
∵BD是正方形ABCD的对角线,
∴AB=
BD=
×2
=
.
故答案为:
.
 解:如图,连接DH、BE,
解:如图,连接DH、BE,∵∠E=∠F=∠G=∠H=60°,
∴DE∥FG∥HB,
∵DE=EF=FG=GH=HB=2,
∴四边形DHBE是平行四边形,
连接BD、EH,设交点为O,
则OE垂直平分FG,
∴OE⊥DE,
∵EF=FG=2,
∴OE=2×
| ||
| 2 |
| 3 |
在Rt△ODE中,OD=
| DE2+OE2 |
22+
|
| 7 |
∴BD=2OD=2
| 7 |
∵BD是正方形ABCD的对角线,
∴AB=
| ||
| 2 |
| ||
| 2 |
| 7 |
| 14 |
故答案为:
| 14 |
点评:本题考查了正方形的性质的运用,平行四边形的判定与性质,等边三角形的性质,勾股定理的应用,难度较大,灵活性较强,作辅助线构造出平行四边形与直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目