题目内容
(2006•黑龙江)已知关于x的一元二次方程kx2-2(k+1)x+k-1=0有两个不相等的实数根x1,x2.(1)求k的取值范围;
(2)是否存在实数k,使
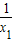 +
+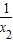 =1成立?若存在,请求出k的值;若不存在,请说明理由.
=1成立?若存在,请求出k的值;若不存在,请说明理由.
【答案】分析:(1)根据一元二次方程的根的判别式,建立关于k的不等式,求得k的取值范围.
(2)利用根与系数的关系,根据 +
+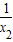 =
= ,即可求出k的值,看是否满足(1)中k的取值范围,从而确定k的值是否存在.
,即可求出k的值,看是否满足(1)中k的取值范围,从而确定k的值是否存在.
解答:解:(1)由题意知,k≠0且△=b2-4ac>0
∴b2-4ac=[-2(k+1)]2-4k(k-1)>0,
即4k2+8k+4-4k2+4k>0,
∴12k>-4
解得:k>- 且k≠0
且k≠0
(2)不存在.
∵x1+x2= ,x1•x2=
,x1•x2=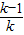 ,
,
又有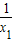 +
+ =
= =1,
=1,
可求得k=-3,而-3<-
∴满足条件的k值不存在.
点评:总结:1、一元二次方程根的情况与判别式△的关系:
①△>0?方程有两个不相等的实数根;
②△=0?方程有两个相等的实数根;
③△<0?方程没有实数根.
2、一元二次方程的根与系数的关系为:x1+x2=- ,x1x2=
,x1x2=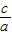
3、一元二次方程的二次项系数不为0
(2)利用根与系数的关系,根据
 +
+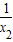 =
= ,即可求出k的值,看是否满足(1)中k的取值范围,从而确定k的值是否存在.
,即可求出k的值,看是否满足(1)中k的取值范围,从而确定k的值是否存在.解答:解:(1)由题意知,k≠0且△=b2-4ac>0
∴b2-4ac=[-2(k+1)]2-4k(k-1)>0,
即4k2+8k+4-4k2+4k>0,
∴12k>-4
解得:k>-
 且k≠0
且k≠0(2)不存在.
∵x1+x2=
 ,x1•x2=
,x1•x2=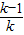 ,
,又有
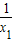 +
+ =
= =1,
=1,可求得k=-3,而-3<-

∴满足条件的k值不存在.
点评:总结:1、一元二次方程根的情况与判别式△的关系:
①△>0?方程有两个不相等的实数根;
②△=0?方程有两个相等的实数根;
③△<0?方程没有实数根.
2、一元二次方程的根与系数的关系为:x1+x2=-
 ,x1x2=
,x1x2=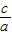
3、一元二次方程的二次项系数不为0

练习册系列答案
相关题目
 =±2
=±2
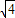 =±2
=±2