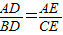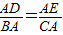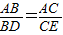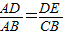题目内容
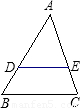
4、如图,能推得DE∥BC的条件是( )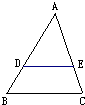

分析:平行于三角形一边的直线截其他两边或延长线,所得的对应线段成比例.如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.
解答:证明:设DE∥BC,
那么,AD:AB=AE:AC,AD:DB=AE:EC,DB:AB=EC:AC,
选项A、B、D、不符合平行线分段成比例定理.
如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,
那么这条直线平行于三角形的第三边.
∵AD:DB=AE:EC,
∴DE∥BC.
故选C.
那么,AD:AB=AE:AC,AD:DB=AE:EC,DB:AB=EC:AC,
选项A、B、D、不符合平行线分段成比例定理.
如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,
那么这条直线平行于三角形的第三边.
∵AD:DB=AE:EC,
∴DE∥BC.
故选C.
点评:此题主要考查学生对平行线分线段成比例的理解和掌握,解答此题的关键的是明确哪些对应线段成比例.学生初学,容易出错.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,下列各比例式不一定能推得DE∥BC的是( )
如图,下列各比例式不一定能推得DE∥BC的是( )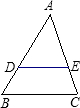 如图,能推得DE∥BC的条件是
如图,能推得DE∥BC的条件是