题目内容
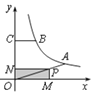
【题目】如图,已知A、B是反比例函数y= k x(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C.过点P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
A.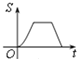 B.
B.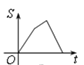 C.
C.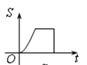 D.
D.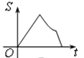
【答案】A.
【解析】
试题分析:设点P的运动速度为v,①由于点A在直线y=x上,故点P在OA上时,四边形OMPN为正方形,四边形OMPN的面积S=![]() ;
;
②点P在反比例函数图象AB时,由反比例函数系数几何意义,四边形OMPN的面积S=k;
③点P在BC段时,设点P运动到点C的总路程为a,则四边形OMPN的面积=![]() OC(a﹣vt)=﹣
OC(a﹣vt)=﹣![]() t+
t+![]() ,纵观各选项,只有A选项图形符合.
,纵观各选项,只有A选项图形符合.
故选A.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目