题目内容
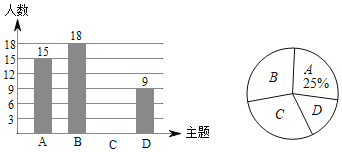
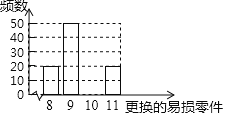
【题目】某种机器使用若干年后即被淘汰,该机器有一易损零件,为调查该易损零件的使用情况,随机抽取了100台已被淘汰的这种机器,经统计:每台机器在使用期内更换的该易损零件数均只有8,9,10,11这四种情况,并整理了这100台机器在使用期内更换的该易损零件数,绘制成如图所示不完整的条形统计图.
(1)请补全该条形统计图;
(2)某公司计划购买一台这种机器以及若干个该易损零件,用上述100台机器更换的该易损零件数的频率代替一台机器更换的该易损零件数发生的概率.
①求这台机器在使用期内共更换了9个该易损零件的概率;
②若在购买机器的同时购买该易损零件,则每个200元;若在使用过程中,因备用该易损零件不足,再购买,则每个500元.请你帮该公司用花在该易损零件上的费用的加权平均数进行决策:购买机器的同时应购买几个该易损零件,可使公司的花费最少?
【答案】(1)补全的条形统计图如图所示,见解析;(2)①这台机器在使用期内共更换了9个该易损零件的概率为![]() ;②购买机器的同时应购买9个该易损零件,可使公司的花费最少.
;②购买机器的同时应购买9个该易损零件,可使公司的花费最少.
【解析】
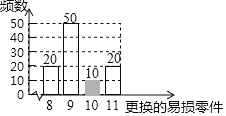
(1)共抽查100台机器,更换8个零件的有20台,更换9个零件的有50台,更换11个零件的有20台,可以计算出更换10个零件的有100-20-50-20=10台,进而补全统计图;
(2)①用样本的频数估计总体的概率,即求出抽查的100台机器中更换9个零件的频率即可;②利用加权平均数计算各种情况下的花费,比较得出答案.
(1)100﹣20﹣50﹣20=10,补全的条形统计图如图所示:
(2)①这台机器在使用期内共更换了9个该易损零件的概率为:P![]() ;
;
②购买机器的同时购买8个该易损零件200×20%+500×80%=440元,
购买机器的同时购买9个该易损零件200×50%+500×50%=350元,
购买机器的同时购买10个该易损零件200×10%+500×90%=470元,
购买机器的同时购买11个该易损零件200×20%+500×80%=440元,
因此,购买机器的同时应购买9个该易损零件,可使公司的花费最少.

【题目】某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
x(元) | 15 | 20 | 30 | … |
y(袋) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数,试求:
(1)日销售量y(袋)与销售价x(元)的函数关系式;
(2)假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?