题目内容
己知反比例函数y=
的图象过点(-2,-
)
①求此函数的解析式;
②如果点A(m,1)是反比例函数图象上的点,求m的值;
③利用②的结果,请在坐标轴上找一点P,使以A、O、P三点为顶点的三角形是直角三角形,请直接写出所有满足条件的点P的坐标.
| k |
| 2x |
| 1 |
| 2 |
①求此函数的解析式;
②如果点A(m,1)是反比例函数图象上的点,求m的值;
③利用②的结果,请在坐标轴上找一点P,使以A、O、P三点为顶点的三角形是直角三角形,请直接写出所有满足条件的点P的坐标.
分析:(1)直接把点(-2,-
)代入反比例函数解析式求出k,即可确定反比例解析式;
(2)把A点坐标代入反比例解析式即可求出m;
(3)作AP1⊥x轴于P1,AP3⊥y轴于P3,利用A点坐标得到P1(1,0),P3(0,1),且△OAP1,OAP3都是等腰直角三角形,当以A、O、P三点为顶点的三角形是以点A为直角顶点的直角三角形时,点P2与O点关于AP1对称,点P4与O点关于AP3对称,则P2(2,0),P4(0,2),
| 1 |
| 2 |
(2)把A点坐标代入反比例解析式即可求出m;
(3)作AP1⊥x轴于P1,AP3⊥y轴于P3,利用A点坐标得到P1(1,0),P3(0,1),且△OAP1,OAP3都是等腰直角三角形,当以A、O、P三点为顶点的三角形是以点A为直角顶点的直角三角形时,点P2与O点关于AP1对称,点P4与O点关于AP3对称,则P2(2,0),P4(0,2),
解答:解:(1)把点(-2,-
)代入y=
,
得-
=
,解得k=2,
所以反比例函数解析式为y=
;
(2)把点A(m,1)代入y=
,得m=1;
(3)如图, 作AP1⊥x轴于P1,AP3⊥y轴于P3,
作AP1⊥x轴于P1,AP3⊥y轴于P3,
∴△OAP1,OAP3都是直角三角形,
而A点坐标为(1,1),
∴P1(1,0),P3(0,1),
∴△OAP1,OAP3都是等腰直角三角形,
∴点A为直角顶点时,点P2与O点关于AP1对称,点P4与O点关于AP3对称,
∴P2(2,0),P4(0,2),
∴满足条件的P点坐标为(1,0),(0,1),(2,0),(0,2).
| 1 |
| 2 |
| k |
| 2x |
得-
| 1 |
| 2 |
| k |
| 2×(-2) |
所以反比例函数解析式为y=
| 1 |
| x |
(2)把点A(m,1)代入y=
| 1 |
| x |
(3)如图,
 作AP1⊥x轴于P1,AP3⊥y轴于P3,
作AP1⊥x轴于P1,AP3⊥y轴于P3,∴△OAP1,OAP3都是直角三角形,
而A点坐标为(1,1),
∴P1(1,0),P3(0,1),
∴△OAP1,OAP3都是等腰直角三角形,
∴点A为直角顶点时,点P2与O点关于AP1对称,点P4与O点关于AP3对称,
∴P2(2,0),P4(0,2),
∴满足条件的P点坐标为(1,0),(0,1),(2,0),(0,2).
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、等腰直角三角形的判定与性质.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
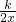 的图象过点(-2,-
的图象过点(-2,- )
) 的图象经过点P(-1,2),则这个函数的图象位于 ( )
的图象经过点P(-1,2),则这个函数的图象位于 ( )