题目内容
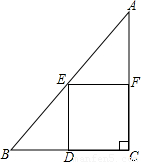
如图是某居民小区的一块直角三角形空地ABC,某斜边AB=100米,直角边AC=80米.现要利用这 块空地建一个矩形停车场DCFE,使得D点在BC边上,E、F分别是AB、AC边的中点.
块空地建一个矩形停车场DCFE,使得D点在BC边上,E、F分别是AB、AC边的中点.(1)求另一条直角边BC的长度;
(2)求停车场DCFE的面积;
(3)为了提高空地利用律,现要在剩余的△BDE中,建一个半圆形的花坛,使它的圆心在BE边上,且使花坛的面积达到最大,请你在原图中画出花坛的草图,求出它的半径(不要求说明面积最大的理由),并求此时直角三角形空地ABC的总利用率是百分之几(精确到1%).
分析:(1)利用勾股定理可求出BC的长;
(2)由已知可得EF为△ABC的中位线,由中位线定理可知EF=
BC=
×60=30m,FC=
AC=
×80=40(米),可求出矩形的面积;
(3)如图,当花坛的面积达到最大时,半圆O与BD、DE相切,设切点分别为G、K,圆心为O,连接OG、OK,则OG⊥BD,OK⊥DE,OG=OK,即四边形OGDK为正方形,设OG=x,易证△OBG∽△ABC,根据其边长比可求出x的值,从而求出半圆的面积,得出结论.
(2)由已知可得EF为△ABC的中位线,由中位线定理可知EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)如图,当花坛的面积达到最大时,半圆O与BD、DE相切,设切点分别为G、K,圆心为O,连接OG、OK,则OG⊥BD,OK⊥DE,OG=OK,即四边形OGDK为正方形,设OG=x,易证△OBG∽△ABC,根据其边长比可求出x的值,从而求出半圆的面积,得出结论.
解答:解:(1)由勾股定理得BC=
=
=60(米),
∴另一条直角边BC的长为60米.
(2)由已知可得EF为△ABC的中位线,
∴EF=
BC=
×60=30(米),
又FC=
AC=
×80=40(米),
∴S矩形DCFE=EF•FC=30×40=1200(米2).
(3)如图,当花坛的面积达到最大时,半圆O与BD、DE相切,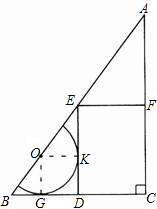
设切点分别为G、K,圆心为O,
连接OG、OK,则OG⊥BD,OK⊥DE,OG=OK,
又∵∠BDE=90°,
∴四边形OGDK为正方形.
设OG=x,
∵BD=BC-CD=60-30=30,
∴BG=BD-GD=30-x.
∵∠OGB=∠C=90°,∠B=∠B,
∴△OBG∽△ABC,
∴
=
.
即
=
=
,解得x=
.
∴当花坛的面积达到最大时,其半径为
米.
∴直角三角形空地ABC的总利用率=[
π(
)2+1200]÷(
×80×60)≈69%.
| AB2-AC2 |
| 1002-802 |
∴另一条直角边BC的长为60米.
(2)由已知可得EF为△ABC的中位线,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
又FC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S矩形DCFE=EF•FC=30×40=1200(米2).
(3)如图,当花坛的面积达到最大时,半圆O与BD、DE相切,

设切点分别为G、K,圆心为O,
连接OG、OK,则OG⊥BD,OK⊥DE,OG=OK,
又∵∠BDE=90°,
∴四边形OGDK为正方形.
设OG=x,
∵BD=BC-CD=60-30=30,
∴BG=BD-GD=30-x.
∵∠OGB=∠C=90°,∠B=∠B,
∴△OBG∽△ABC,
∴
| OG |
| BG |
| AC |
| BC |
即
| x |
| 30-x |
| 80 |
| 60 |
| 4 |
| 3 |
| 120 |
| 7 |
∴当花坛的面积达到最大时,其半径为
| 120 |
| 7 |
∴直角三角形空地ABC的总利用率=[
| 1 |
| 2 |
| 120 |
| 7 |
| 1 |
| 2 |
点评:本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力.
利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目