题目内容
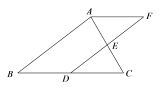
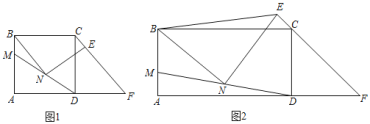
【题目】在矩形ABCD中,点F在AD延长线上,且DF=DC,M为AB边上一点,N为MD的中点,点E在直线CF上,且BN=NE.
(1)如图1,若AB=BC=6,BM=![]() AB,E为线段FC上的点,试求NE的长;
AB,E为线段FC上的点,试求NE的长;
(2)如图2,若AB<BC,E为线段FC延长线上的点,连结BE,求证:BE=![]() NE.
NE.
【答案】(1)NE=5;(2)证明见解析
【解析】
(1)延长BN交CD的延长线于点G,连接BE、GE,过E作EH⊥CE,由AAS证明△BMN≌△GDN,得出BM=DG,BN=GN,由勾股定理求出BG,即可得出答案;
(2)延长BN交CD的延长线于点G,连接GE,GE交AD于点Q,过E作EH⊥CE,交DC的延长线于点H,由AAS证得△BMN≌△GDN,得出BN=NG=NE,则△BEG是直角三角形,∠BEG=90°,再由ASA证得△ECB≌△EHG得出EB=EG,证得△BNE是等腰直角三角形,即可得出结论.
(1)解:延长BN交CD的延长线于点G,连接BE、GE,过E作EH⊥CE,交CD于点H.
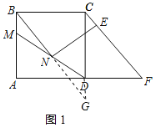
∵四边形ABCD是矩形,AB=BC=6,
∴∠BCD=90°,AB∥CG,四边形ABCD是正方形,
∴∠MBN=∠DGN,CD=BC=6,
∵N为MD的中点,
∴MN=DN.在△BMN和△GDN中,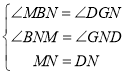 ,
,
∴△BMN≌△GDN(AAS).
∴BM=DG,BN=GN.
∵BM=![]() AB=2,
AB=2,
∴DG=2,
∴CG=CD+DG=8,
在Rt△BCG中,由勾股定理得:BG=![]() =
=![]() =10,
=10,
∴BN=![]() BG=5,
BG=5,
∵BN=NE,
∴NE=5;
(2)证明:延长BN交CD的延长线于点G,连接GE,GE交AD于点Q,过E作EH⊥CE,交DC的延长线于点H,如图2所示:
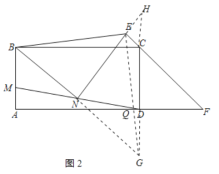
∵四边形ABCD是矩形,
∴AB∥CG,
∴∠MBN=∠DGN,∠BMN=∠GDN,
∵N为MD的中点,
∴MN=DN,
在△BMN和△GDN中,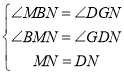 ,
,
∴△BMN≌△GDN(AAS),
∴BN=NG=NE,
∴△BEG是直角三角形,∠BEG=90°,
∵EH⊥CE,
∴∠CEH=90°.
∴∠BEG=∠CEH,
∴∠BEC=∠GEH,
∵DF=DC,∠CDF=90°,
∴∠DCF=45°,
∴∠CHE=∠HCE=45°,
∴EC=EH,
∵∠ECB=∠HCB﹣∠HCE=90°﹣45°=45°,
∴∠ECB=∠EHG,在△ECB和△EHG中,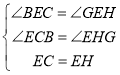 ,
,
∴△ECB≌△EHG(ASA),
∴EB=EG,
∵BN=NG,
∴BN⊥NE,
∴△BNE是等腰直角三角形,
∴BE=![]() NE.
NE.