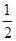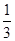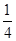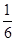题目内容
在一个不透明的口袋中装有4张相同的纸牌,它们分别标有数字1,2,3,4.随机地摸取出一张纸牌然后放回,再随机摸取出一张纸牌.
(1)用树状图或列表的方法计算两次摸取纸牌上数字之积为奇数的概率;
(2)甲、乙两个人进行游戏,如果两次摸出纸牌上数字之积为奇数,则甲胜;如果两次摸出纸牌上数字之积为偶数,则乙胜。这个游戏公平吗?如果公平,请说明理由.如果不公平,请设计一种游戏规则,使得游戏对双方公平.
(1)用树状图或列表的方法计算两次摸取纸牌上数字之积为奇数的概率;
(2)甲、乙两个人进行游戏,如果两次摸出纸牌上数字之积为奇数,则甲胜;如果两次摸出纸牌上数字之积为偶数,则乙胜。这个游戏公平吗?如果公平,请说明理由.如果不公平,请设计一种游戏规则,使得游戏对双方公平.
(1)列表见解析, ,(2)游戏不公平,可改为如下:两次摸出纸牌上数字之和为奇数,则甲胜;和为偶数,则乙胜
,(2)游戏不公平,可改为如下:两次摸出纸牌上数字之和为奇数,则甲胜;和为偶数,则乙胜
 ,(2)游戏不公平,可改为如下:两次摸出纸牌上数字之和为奇数,则甲胜;和为偶数,则乙胜
,(2)游戏不公平,可改为如下:两次摸出纸牌上数字之和为奇数,则甲胜;和为偶数,则乙胜(1)列表如下(也可以用树状图):
………………..3分
P(积为奇数)= ………………..5分
………………..5分
(2)∵P(积为奇数)= ,P(积为偶数)=
,P(积为偶数)=
∴游戏不公平 ………………..7分
可改为如下:两次摸出纸牌上数字之和为奇数,则甲胜;和为偶数,则乙胜(方法不唯一)………………..10分
(1)列举出所有情况,看摸出的这两个数的积为6的情况占总情况的多少即可;
(2)看两个数的积为奇数的情况占所有情况的多少即可求得小敏赢的概率,进而求得小颖赢的概率,比较即可.
| 积 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 4 | 6 | 8 |
| 3 | 3 | 6 | 9 | 12 |
| 4 | 4 | 8 | 12 | 16 |
P(积为奇数)=
 ………………..5分
………………..5分(2)∵P(积为奇数)=
 ,P(积为偶数)=
,P(积为偶数)=
∴游戏不公平 ………………..7分
可改为如下:两次摸出纸牌上数字之和为奇数,则甲胜;和为偶数,则乙胜(方法不唯一)………………..10分
(1)列举出所有情况,看摸出的这两个数的积为6的情况占总情况的多少即可;
(2)看两个数的积为奇数的情况占所有情况的多少即可求得小敏赢的概率,进而求得小颖赢的概率,比较即可.

练习册系列答案
相关题目
 ,朝下一面的数为
,朝下一面的数为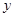 ,得到平面直角坐标系中的一个点
,得到平面直角坐标系中的一个点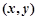 .已知小华前二次掷得的两个点所确定的直线经过点
.已知小华前二次掷得的两个点所确定的直线经过点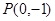 ,则他第三次掷得的点也在这条直线上的概率为 .
,则他第三次掷得的点也在这条直线上的概率为 . 
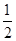
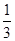
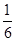
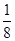
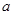 是实数,
是实数,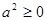 ”这一事件是___________事件.
”这一事件是___________事件.