题目内容
 如图所示,某人到岛上去探宝,从A处登陆后先往东走4km,又往北走1.5km,遇到障碍后又往西走2km,再转向北走到4.5km处往东一拐,仅走0.5km就找到宝藏.问登陆点A与宝藏埋藏点B之间的距离是多少?
如图所示,某人到岛上去探宝,从A处登陆后先往东走4km,又往北走1.5km,遇到障碍后又往西走2km,再转向北走到4.5km处往东一拐,仅走0.5km就找到宝藏.问登陆点A与宝藏埋藏点B之间的距离是多少?
 解:过点B作BC⊥AD于C,则AC=4-2+0.5=2.5km,BC=6km,
解:过点B作BC⊥AD于C,则AC=4-2+0.5=2.5km,BC=6km,在Rt△ABC中,由勾股定理求得AB=
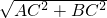 =
= =6.5(km).
=6.5(km).所以登陆点A与宝藏埋藏点B之间的距离是6.5km.
分析:本题需要把实际问题转化为数学模型,过点B作过点A的直线的垂线,构造直角三角形,利用勾股定理完成.
点评:本题的关键是把实际问题转化为数学模型,运用勾股定理进行求解.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
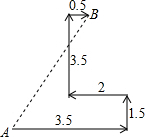 如图所示,某人到岛上去探宝,从A处登陆后先往东走3.5km,又往北走1.5km,遇到障碍后又往西走2km,再转向北走到3.5km处往东一拐,仅走0.5km就找到宝藏,则登陆点A与宝藏埋藏点B之间的距离是
如图所示,某人到岛上去探宝,从A处登陆后先往东走3.5km,又往北走1.5km,遇到障碍后又往西走2km,再转向北走到3.5km处往东一拐,仅走0.5km就找到宝藏,则登陆点A与宝藏埋藏点B之间的距离是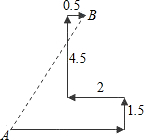 如图所示,某人到岛上去探宝,从A处登陆后先往东走4km,又往北走1.5km,遇到障碍后又往西走2km,再转向北走到4.5km处往东一拐,仅走0.5km就找到宝藏.问登陆点A与宝藏埋藏点B之间的距离是多少?
如图所示,某人到岛上去探宝,从A处登陆后先往东走4km,又往北走1.5km,遇到障碍后又往西走2km,再转向北走到4.5km处往东一拐,仅走0.5km就找到宝藏.问登陆点A与宝藏埋藏点B之间的距离是多少?
