题目内容
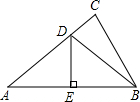
如下图,△ABC的高AD与CE交于点F且AD=CD.
求证:(1)AB=CF
(2)当AE=![]() CF时△ABC是等腰三角形.
CF时△ABC是等腰三角形.
答案:
解析:
解析:
|
(1)在△AEF和△CDF中 ∠AEF=∠CDF= ∠AFE=∠CFD ∴∠EAF=∠DCF 在△ABD和△CFD中 ∠ADB=∠CDF,∠BAD=∠DCF,AD=CD ∴△ABD≌△CFD(ASA) ∴AB=CF (2)由(1)知△ABD≌△CFD ∴AB=CF ∵AE= ∴AE= ∴AE=BE ∵CE⊥AB ∴∠AEC=∠BEC= 在△AEC和△BEC中AE=BE,∠AEC=∠BEC= ∴△AEC≌△BEC ∴AC=BC ∴△ABC为等腰三角形 |

练习册系列答案
相关题目
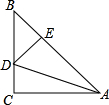 如下图,△ABC中,∠C=90°,∠B=45°,AD是角平分线,DE⊥AB于E,则下列结论不正确的是( )
如下图,△ABC中,∠C=90°,∠B=45°,AD是角平分线,DE⊥AB于E,则下列结论不正确的是( )| A、AC=AE | B、CD=DE | C、CD=DB | D、AB=AC+CD |
 9、如下图,△ABC的角平分线BE,CD交于点P,∠DPE=120°,则∠A的大小等于( )
9、如下图,△ABC的角平分线BE,CD交于点P,∠DPE=120°,则∠A的大小等于( ) 12、如下图,△ABC中,AB的垂直平分线交AC于D,如果AC=5cm,BC=4cm,那么△DBC的周长是( )
12、如下图,△ABC中,AB的垂直平分线交AC于D,如果AC=5cm,BC=4cm,那么△DBC的周长是( )