��Ŀ����
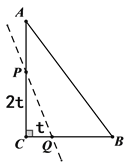
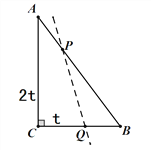
����Ŀ����ͼ����ABC�У���C=90�㣬AB=10cm��BC=6cm��������P�ӵ�C��ʼ����C��A��B��C��·���˶������ٶ�Ϊÿ��2 cm/s�����˶���ʱ��Ϊt�룮
��1�������������BCP�ǵ���ֱ�������Σ���˵�����ɡ�
��2����t=_____________________ʱ����BCPΪ���������Σ�
��3������һ��Q���ӵ�C��ʼ����C��B��·���˶������ٶ�Ϊ1cm/s����P��Q����ͬʱ��������P��Q����һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶�����tΪ��ֵʱ��ֱ��PQ����ABC���ܳ��ֳɵ�������֮����2����ϵ��



(����ͼ) (����ͼ)
���𰸡�(1)t=3,���ɼ���������2��3s, 5.4s, 6s��6.5s����3��t=![]() ��t=
��t=![]() .
.
�������������������1��������ó�BC=CP�����ɵó������
��2����BCPΪ����������ʱ������������������ۣ���CP=CB����BC=BP����PB=PC�����ɵó��𰸣�
��3����P��Q����һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶����ó�0��t��6��C��ABC=24����ֱ��PQ�ѡ�ABC���ܳ��ֳɵ�������֮����1��2����һ����Ϊ8����һ����Ϊ16����������������ɵó��𰸣�
���������
(1) ����BCP�ǵ���ֱ��������
��BC=CP
��2t=6
t=3s
��2����t= 3s, 5.4s, 6s��6.5s ʱ����BCPΪ����������.
��3����P��Q����һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶���
��0��t��6
C��ABC=24
��ֱ��PQ�ѡ�ABC���ܳ��ֳɵ�������֮����1��2
��һ����Ϊ8����һ����Ϊ16
��t+2t=8, t=![]()
��t+2t=16, t=![]()