题目内容
 16、如图,这是一个由三个大小不同的正方体所组成的装饰物,现在要对它的表面涂油漆、假设三个正方体的边长分别为a,b,c,其中a<b<c、那么该装饰物涂漆面积最少(当该装饰物水平放置在桌面上的时候,不能从外观上看见装饰物的任何裸露)是
16、如图,这是一个由三个大小不同的正方体所组成的装饰物,现在要对它的表面涂油漆、假设三个正方体的边长分别为a,b,c,其中a<b<c、那么该装饰物涂漆面积最少(当该装饰物水平放置在桌面上的时候,不能从外观上看见装饰物的任何裸露)是5a2+4b2+4c2
.分析:解此类题首先要计算表面积,即从上面看到的面积+四个侧面看到的面积+下面看到的面积.
解答:解:根据分析其表面积=a2+b2+c2+2a2+2(a2+b2+c2)+b2+c2=5a2+4b2+4c2,即涂上颜色的面积最少为5a2+4b2+4c2.
故答案为:5a2+4b2+4c2.
故答案为:5a2+4b2+4c2.
点评:主要考查了立体图形的视图问题.解题的关键是能把从不同的方向上看到的图形面积抽象出来(即利用视图的原理),从而求得总面积.

练习册系列答案
相关题目
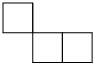
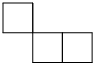 17、如图,这是由三个正方形构成的图形.请你在这个图形中再添加一个正方形,使得添加完之后的图形是一个轴对称图形.
17、如图,这是由三个正方形构成的图形.请你在这个图形中再添加一个正方形,使得添加完之后的图形是一个轴对称图形.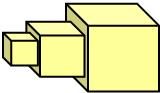 如图,这是一个由三个大小不同的正方体所组成的装饰物,现在要对它的表面涂油漆、假设三个正方体的边长分别为a,b,c,其中a<b<c.那么该装饰物涂漆面积最少(当该装饰物水平放置在桌面上的时候,不能从外观上看见装饰物的任何裸露)是________.
如图,这是一个由三个大小不同的正方体所组成的装饰物,现在要对它的表面涂油漆、假设三个正方体的边长分别为a,b,c,其中a<b<c.那么该装饰物涂漆面积最少(当该装饰物水平放置在桌面上的时候,不能从外观上看见装饰物的任何裸露)是________. 如图,这是由三个正方形构成的图形.请你在这个图形中再添加一个正方形,使得添加完之后的图形是一个轴对称图形.
如图,这是由三个正方形构成的图形.请你在这个图形中再添加一个正方形,使得添加完之后的图形是一个轴对称图形.