题目内容
已知平行四边形的一边长为10,则对角线的长度可能取下列数组中的( )
分析:根据题意画出图形,由四边形ABCD是平行四边形,可得OA=
AC,OB=
BD,又由AB=10,利用三角形的三边关系,即可求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答: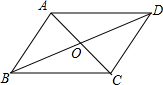 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴OA=
AC,OB=
BD,
∵AB=10,
A、∵AC=4,BD=8,
∴OA=2,OB=4,
∵OA+OB=6<10,
∴不能组成三角形,
故本选项错误;
B、∵AC=10,BD=32,
∴OA=5,OB=15,
∵OA+AB=15<16,
∴不能组成三角形,
故本选项错误;
C、∵AC=8,BD=10,
∴OA=4,OB=5,
∵OA+OB=9<10,
∴不能组成三角形,
故本选项错误;
D、∵AC=11,BD=13,
∴OA=5.5,OB=6.5,
∵OA+OB=14>10,
∴能组成三角形,
故本选项正确.
故选D.
 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,∴OA=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=10,
A、∵AC=4,BD=8,
∴OA=2,OB=4,
∵OA+OB=6<10,
∴不能组成三角形,
故本选项错误;
B、∵AC=10,BD=32,
∴OA=5,OB=15,
∵OA+AB=15<16,
∴不能组成三角形,
故本选项错误;
C、∵AC=8,BD=10,
∴OA=4,OB=5,
∵OA+OB=9<10,
∴不能组成三角形,
故本选项错误;
D、∵AC=11,BD=13,
∴OA=5.5,OB=6.5,
∵OA+OB=14>10,
∴能组成三角形,
故本选项正确.
故选D.
点评:此题考查了平行四边形的性质以及三角形的三边关系.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知平行四边形的一边长为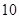 ,则对角线的长度可能取下列数组中的( )
,则对角线的长度可能取下列数组中的( )
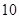 ,则对角线的长度可能取下列数组中的( )
,则对角线的长度可能取下列数组中的( )A.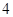 、 、 | B. 、 、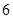 | C. 、 、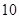 | D.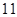 、 、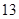 |
已知平行四边形的一边长是14,下列各组数中能分别作为它的两条对角线的是( )
| A.10与16 | B.12与16 | C.20与22 | D.10与40 |
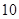 ,则对角线的长度可能取下列数组中的( )
,则对角线的长度可能取下列数组中的( )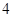 、
、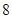 B.
B.  C.
C. 、
、