题目内容
【题目】如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于F,与DC的延长线相交于点H.
(1)求证:△BEF≌△CEH;
(2)求DE的长.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)由平行四边形的性质得出AB∥CD,由AAS证明△BEF≌△CEH即可;
(2)由平行四边形的性质得出CD=AB=3,BC=AD=4,AB∥CD,由平行线的性质得出∠HCE=∠B=60°,证出EF⊥DH,由含30°角的直角三角形的性质得出CH=![]() CE=1,求出EH=
CE=1,求出EH=![]() ,DH=CD+CH=4,由勾股定理求出DE即可.
,DH=CD+CH=4,由勾股定理求出DE即可.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵EF⊥AB
∴EF⊥CD,
∴∠BFE=∠CHE=90°,
∵E是BC的中点,
∴BE=CE,
在△BEF和△CEH中,
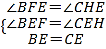 ,
,
∴△BEF≌△CEH(AAS);
(2)∵∠B=∠HCE=60,∠BFE=∠H=90
∴CH=![]() CE=
CE=![]() BC=
BC=![]() AD=1
AD=1
EH=![]()
∴DH=DC+CH=AB+CH=3+1=4
∴在Rt△DEH中,DE=![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】乐乐的爸爸投资股票,有一次乐乐发现爸爸持有股票的情况如表格所示:
股票名称 | 每股净赚(元) | 股数 |
天河 | ﹣22 | 500 |
北斗 | +1.5 | 1000 |
白马 | ﹣4 | 1000 |
海湖 | ﹣(﹣2) | 500 |
请你帮助乐乐爸爸究竟是赚了还是赔了,赚或赔了多少元?


