题目内容
(2012•开平区一模)如图,有3张背面相同的纸牌A,B,C,其正面分别画有三个不同的几何图形.
(1)求摸出一张纸片恰好是画有圆的概率;
(2)将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.求摸出两张牌面图形都是中心对称图形的纸牌的概率.(用树状图或列表法求解,纸牌可用A,B,C表示)
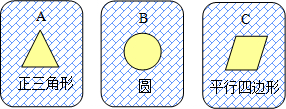
(1)求摸出一张纸片恰好是画有圆的概率;
(2)将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.求摸出两张牌面图形都是中心对称图形的纸牌的概率.(用树状图或列表法求解,纸牌可用A,B,C表示)

分析:(1)根据3张背面相同的纸牌A,B,C,只有一张纸片画着圆,即可求出得到圆的概率;
(2)采用树状图或列表法求解,由于B(圆)与C(平行四边形)是中心对称图形,可得摸出两张牌面图形都是中心对称图形的纸牌的有4种,继而利用概率公式即可求得答案.
(2)采用树状图或列表法求解,由于B(圆)与C(平行四边形)是中心对称图形,可得摸出两张牌面图形都是中心对称图形的纸牌的有4种,继而利用概率公式即可求得答案.
解答:解:(1)∵3张背面相同的纸牌A,B,C,只有一张纸片画着圆,
∴P(圆)=
;
(2)画树状图如下:
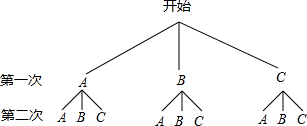
从树状图可以看出,所有可能出现的结果共有9个,
这些结果出现的可能性相等,而在三张纸片中的正三角形、圆、平行四边形中,中心对称图形是圆和平行四边形,
所以两张都是中心对称图形的结果有4个,
则P(两次中心对称图形)=
.
∴P(圆)=
| 1 |
| 3 |
(2)画树状图如下:

从树状图可以看出,所有可能出现的结果共有9个,
这些结果出现的可能性相等,而在三张纸片中的正三角形、圆、平行四边形中,中心对称图形是圆和平行四边形,
所以两张都是中心对称图形的结果有4个,
则P(两次中心对称图形)=
| 4 |
| 9 |
点评:此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.

练习册系列答案
相关题目
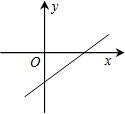 (2012•开平区一模)如果一次函数y=(a-1)x+b的图象如图所示,那么a的取值范围是( )
(2012•开平区一模)如果一次函数y=(a-1)x+b的图象如图所示,那么a的取值范围是( )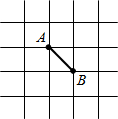 (2012•开平区一模)如图所示的正方形网格中,网格线的交点称为格点.已知A、B是格点,若C也是格点,且△ABC为等腰三角形,则满足条件的点C的个数是( )
(2012•开平区一模)如图所示的正方形网格中,网格线的交点称为格点.已知A、B是格点,若C也是格点,且△ABC为等腰三角形,则满足条件的点C的个数是( ) (2012•开平区一模)如图,在直角三角形纸片ABC中,∠A=90°,剪去这个直角后得到一个四边形,则∠BEF+∠CFE的度数是
(2012•开平区一模)如图,在直角三角形纸片ABC中,∠A=90°,剪去这个直角后得到一个四边形,则∠BEF+∠CFE的度数是