题目内容
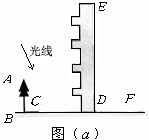
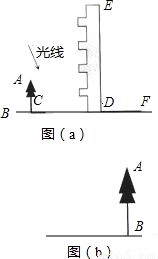
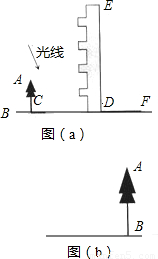
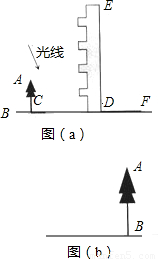
 高为12米的教学楼ED前有一棵大树AB,如图(a).
高为12米的教学楼ED前有一棵大树AB,如图(a).
(1)某一时刻测得大树AB、教学楼ED在阳光下的投影长分别是BC=2.5米,DF=7.5米,求大树AB的高度;
(2)现有皮尺和高为h米的测角仪,请你设计另一种测量大树AB高度的方案,要求:
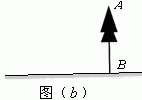
①在图(b)中,画出你设计的测量方案示意图,并将应测量的数据标记在图上(长度用字母m,n …表示,角度用希腊字母α,β …表示);
②根据你所画出的示意图和标注的数据,求出大树的高度.(用字母表示)
解:(1)连接AC,EF,则△ABC∽△EDF,
∴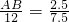 ,
,
∴AB=4,
即大树AB高是4米.
(2)解法一:
①如图(b)(标注m,α,画草图也可给相同的分);
②在Rt△CMA中,∵AM=CMtanα=mtanα,
∴AB=mtanα+h.
解法二:
①如图(c)(标注m,α,β,画草图也可给相同的分);
②AMcotα-AMcotβ=m,
∴AM=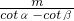 ,
,
∴AB=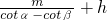 .
.
分析:此题考查了学生学以致用的能力,考查了学生利用数学知识解决实际问题的能力;解此题的关键是利用相似三角形的性质,相似三角形的对应边成比例求解.解题时还要注意认识图形.
点评:本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出树的高度,体现了方程的思想.还要注意学以致用,注意知识的积累.
∴
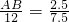 ,
,∴AB=4,
即大树AB高是4米.
(2)解法一:
①如图(b)(标注m,α,画草图也可给相同的分);
②在Rt△CMA中,∵AM=CMtanα=mtanα,
∴AB=mtanα+h.
解法二:
①如图(c)(标注m,α,β,画草图也可给相同的分);
②AMcotα-AMcotβ=m,
∴AM=
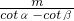 ,
,∴AB=
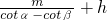 .
.
分析:此题考查了学生学以致用的能力,考查了学生利用数学知识解决实际问题的能力;解此题的关键是利用相似三角形的性质,相似三角形的对应边成比例求解.解题时还要注意认识图形.
点评:本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出树的高度,体现了方程的思想.还要注意学以致用,注意知识的积累.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
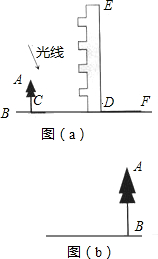 高为12米的教学楼ED前有一棵大树AB,如图(a).
高为12米的教学楼ED前有一棵大树AB,如图(a).