Question

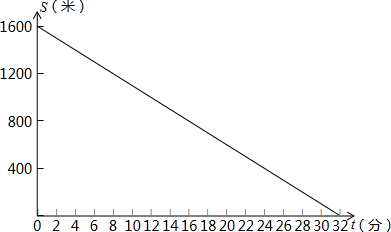
张勤同学的父母在外打工，家中只有年迈多病的奶奶．星期天早上，李老师从家中出发步行前往张勤家家访．6分钟后，张勤从家出发骑车到相距1200米的药店给奶奶买药，停留14分钟后以相同的速度按原路返回，结果与李老师同时到家．张勤家、李老师家、药店都在东西方向笔直大路上，且药店在张勤家与李老师家之间．在此过程中设李老师出发t（0≤t≤32）分钟后师生二人离张勤家的距离分别为S₁、S₂．S₁与t之间的函数关系如图所示，请你解答下列问题：
（1）李老师步行的速度为______；
（2）求S₂与t之间的函数关系式，并在如图所示的直角坐标系中画出其函数图象；
（3）张勤出发多长时间后在途中与李老师相遇？

Answer 1

【答案】分析：（1）根据速度=，再结合图形，即可求出李老师步行的速度；
（2）根据题意分0≤t≤6，6＜t≤12，12＜t≤26，26＜t≤32四种情况进行讨论，即可得出S₂与t之间的函数关系式；
（3）由S₁=S₂得，200t-1200=-50t+1600，然后求出t的值即可；
解答：解：（1）李老师步行的速度为1600÷32=50米/分；
故答案为：50米/分．

（2）根据题意得：
当0≤t≤6时，S₂=0，
当6＜t≤12时，S₂=200t-1200，
当12＜t≤26时，S₂=1200，
当26＜t≤32时，S₂=-200t+6400，


（3）S₁=-50t+1600，
由S₁=S₂得，200t-1200=-50t+1600，
解得t=11.2，
可得t-6=11.2-6=5.2（分）
则张勤出发5.2分钟后在途中与李老师相遇．
点评：此题考查了一次函数的应用，此类题是近年中考中的热点问题，在此题中作图的关键是联系实际的变化，确定拐点．