题目内容
【题目】如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC,
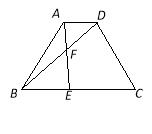
(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)根据条件∠BAE=∠DBC,再证明∠ABE=∠C,可得出结论;(2)分别过点A、D向BC边作垂线段,垂足分别为点G、H,证明△ABG≌△DCH 得出BG=HC,然后求出BH=2,利用勾股定理求出HD,然后利用正切的定义计算即可;(3)根据△ABE∽△BCD求出BE=![]() ,利用勾股定理求出BD的长,再根据
,利用勾股定理求出BD的长,再根据![]() =
=![]() ,求出BF的长.
,求出BF的长.
试题解析:(1)∵等腰梯形ABCD中,AD∥BC,∴∠ABE=∠C
又∵∠BAE=∠DBC ∴△ABE∽△BCD
(2)分别过点A、D向BC边作垂线段,垂足分别为点G、H
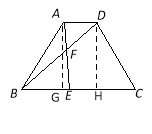
∵AD∥BC ∴AG=DH, 矩形AGHD中AG=DH,
又∵AB=CD∴△ABG≌△DCH ∴BG=HC
∵AD=1,BC=3 ,GH =1∴HC=(3-1)÷2=1, BH=2
∴在Rt△HDC中, HD=![]() =
=![]()
∴在Rt△BHD中, tan∠DBC=![]() =
=![]()
(3)∵△ABE∽△BCD ∴![]()
又∵BC=3,AB=CD=2,∴BE=![]()
∵AD∥BC , AD=1,![]() =
=![]()
又∵BD=![]() =
=![]() , ∴BF =
, ∴BF =![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




